Пример. Для исследования выходного параметра технологического процесса при числе параметров k=2 был спланирован ПФЭ и выполнено три серии параллельных экспериментов

Для исследования выходного параметра технологического процесса при числе параметров k =2 был спланирован ПФЭ 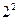и выполнено три серии параллельных экспериментов. Использовались следующие значения нулевых уровней 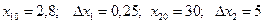. Результаты эксперимента представлены в табл.2.7.

Таблица 2.7

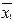
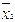
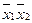
Номер эксперимента				Результат отклика в параллельных опытах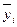
	-	-	-
	-	+	+
	+	-	-
	+	+	+

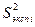
Требуется построить модель, описывающую выходной параметр технологического процесса, проверить ее адекватность.

Эксперимент проводится при двух значениях фактора

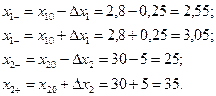
Для облегчения расчетов удобно провести нормировку факторов с помощью преобразований

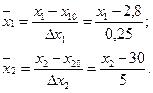(2.29)

По формулам (2.18) и (2.19) посчитываем среднее значение и дисперсии в каждом эксперименте матрицы

.

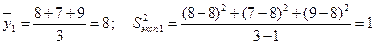Результаты расчета величин 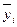и 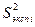внесены в табл.2.6. Применяя критерий Кохрена, нетрудно убедиться, что опыты воспроизводимы, т.к.

.

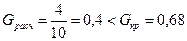По формуле (2.22) находим дисперсию воспроизводимости опытов

.

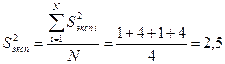Используя формулы (2.23) определим коэффициенты уравнения регрессии

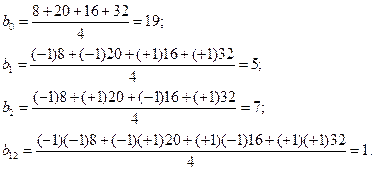
Проверяем значимость коэффициентов. По таблицам распределения критерия Стьюдента при 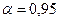и числе степеней свободы

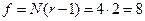
находим .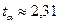

Определяем 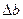по формуле (2.25)

.

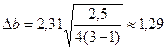Так как выполняются условия

,

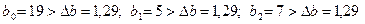то коэффициенты 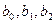значимы, а коэффициент 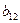незначим, так как для него условие 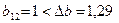не выполняется.

Линейная модель запишется в виде

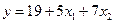. (2.30)

Проверим адекватность этой модели. По формуле (2.26) подсчитаем дисперсию, характеризующую ошибку модели. Для получения значений 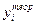, используемых в формуле (2.26), в записанную модель (2.30) подставляем кодированные значения факторов 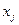согласно матрице плана (табл.2.6). Например, для первого эксперимента (строки) матрицы имеем:

.

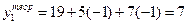Аналогично находим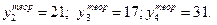

Используя формулу (2.26) определяем дисперсию, характеризующую ошибку модели

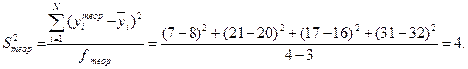
Расчетное значение критерия Фишера находим по выражению (2.27)

.

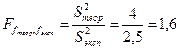По таблице критерия Фишера для доверительной вероятности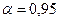

по значениям числа степеней свободы 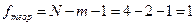и 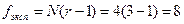находим .

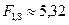Так как условие (1,6<5,32), то линейная модель вида (2.30) адекватна результатам эксперимента и ею можно пользоваться на практике.

Осуществим переход к размерному полиному, используя соотношение (2.29), значения нулевых уровней и интервалов варьирования факторам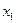и и .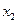

Получаем

.

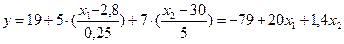Методика использования полного факторного эксперимента показана на примере выполнения лабораторной работы 2.

Дата добавления: 2014-01-03