Проверка адекватности системы

Анализ результатов моделирования

Первый вопрос, который нас интересует после проведения эксперимента и вычисления коэффициентов модели – это проверка адекватности. С этой целью вычисляем остаточную дисперсию или дисперсию адекватности:

,

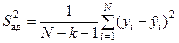где 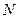— количество опытов в эксперименте;

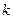— количество факторов;

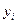— экспериментальные значения отклика;

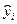— величина отклика, предсказанная уравнением регрессии.

Для проверки гипотезы об адекватности модели пользуются 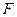- критерием Фишера, т.е. вычисляется соотношение:

,

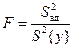где 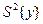— это выборочная дисперсия, которая вычисляется по формуле:

,

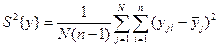где 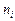— количество повторений одного опыта;

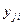— экспериментальное значение отклика в 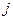-м опыте при 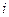-м наблюдении;

.

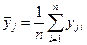Если рассчитанное значение 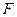- критерия не превышает табличного, то с соответствующей доверительной вероятностью модель можно считать адекватной.

Рассмотренный способ расчета дисперсии адекватности применим в случае, если опыты в матрице планирования не дублируются, а информация о выборочной дисперсии извлекается из параллельных опытов в нулевой точке или из предварительных экспериментов. В общем случае,

,

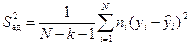где 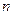— число повторений 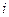-го опыта;

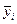— среднее арифметическое отклика из 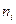параллельных опытов.

Здесь смысл введения 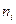в формулу заключается в следующем: различию между экспериментальным и расчетным значением придается тем больший вес, чем больше число повторных опытов.

Адекватность линейного уравнения можно проверить и другим путем. Очевидно, что коэффициент 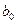, определенный по результатам полного или дробного факторного эксперимента, всегда является оценкой:

.

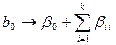С другой стороны, величина 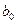является оценкой результата опыта на основном уровне. Поэтому, если выполнить опыт на основном уровне, т.е. получить 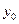и найти разницу 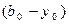, то эта величина является оценкой суммы квадратичных членов в уравнении регрессии. Если разность 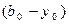велика, линейным уравнением пользоваться нельзя, если мала – возможность использования линейного уравнения не исключена. Значимость различия можно оценить по критерию Стьюдента:

,

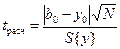где 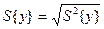— выборочное среднеквадратическое отклонение.

Гипотеза об адекватности уравнения принимается в случае, когда .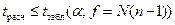

Дата добавления: 2014-01-03