Что такое размерность?

Размерность это формализованное отражением качественного различия физических величин является их. Размерность обозначается символом dim, происходящим от слова dimension, которое в зависимости от контекста может переводиться и как размер, и как размерность.

Размерность основных физических величин обозначается соответствующими заглавными буквами. Для длины, массы и времени, например,

dim I = L; dim m = M; dim t = Т.

35. Каковы правила определения размерности производных величин?

Для определения размерностипроизводных величин используют правила:

1. Размерности правой и левой частей уравнения не могут не совпадать, т.к. сравниваться между собой могут только одинаковые свойства. Алгебраически могут суммироваться только величины, имеющие одинаковые размерности.

2. Алгебра размерностей мультипликативна, т.е. состоит из одного единственного действия - умножения.

2.1. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между значениями величин Q, А, В, С имеет вид Q=АВС, то

dim Q = dim A • dim В • dim С.

2.2. Размерность частного при делении одной величины на другую равна отношению их размерностей, т.е. если Q=A/B, то

dim Q = dim A / dim В.

2.3. Размерность любой величины, возведенной в некоторую степень, равна ее размерности в той же степени. Так, если Q=Aⁿ, то

dim Q = 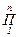dim A = dimⁿA.

Например, если скорость определять по формуле v = S/t, то dim v=dim S/dim t = L/T=LT^-1. Если сила по второму закону Ньютона F=ma, где a=v/t - ускорение тела, то

dim F = dim m dim a = ML/T² = MLT^-2.

Таким образом, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью степенного одночлена:

dim Q = L^aM^bT^g...,

где L, М, Т,... - размерности соответствующих основных физических величин; a, b, g,... - показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулем. Если все показатели размерности равны нулю, то такая величина называется безразмерной. Она может быть относительной, определяемой как отношение одноименных величин (например, относительная диэлектрическая проницаемость), и логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).

Теория размерности повсеместно применяется для оперативной проверки правильности формул (по правилу 1). Формальное применение алгебры размерностей иногда позволяет определить неизвестную зависимость между физическими величинами.

4 ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

Погрешность результата измерения – это отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Истинное значение величины неизвестно, его применяют только в теоретических исследованиях. На практике используют действительное значение величины х_д. Тогда погрешность измерения Δх_изм определяется по формуле:

Δх_изм = х_изм – х_д, (5.1)

где х_изм – измеренное значение величины.

По способу выражения погрешности измерений можно разделить на абсолютные и относительные. Абсолютная погрешность выражается в единицах измеряемой величины и определяется по формуле (5.1).

Относительная погрешность выражается отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины. Относительную погрешность в долях или процентах находят из отношений:

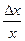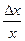
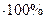δ = ; δ = (5.2)

где Δх – абсолютная погрешность измерений;

х – действительное или измеренное значение величины.

Погрешности можно разделить по признакам:

· по способу выражения – абсолютные и относительные;

· по характеру проявления – систематические и случайные;

· по условиям измерения измеряемой величины – погрешность воспроизведения единицы, хранения единицы, передачи размера единицы физической величины.

По характеру проявления погрешности делятся на систематические и случайные. Систематическая погрешность измерения – это составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. В зависимости от характера изменения систематические погрешности подразделяют на постоянные, прогрессивные, периодические и погрешности, изменяющиеся по сложному закону. Систематические погрешности должны быть определены и исключены из результатов измерений введением поправки – величины, равной по абсолютному значению систематической погрешности и противоположной ей по знаку.

Случайная погрешность измерения – это составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и тоже физической величины.

Характеристиками систематических погрешностей являются: значение (для постоянной погрешности), функция определения (для переменной погрешности).

Случайные погрешности можно описать:

– вероятностными характеристиками;

– распределением (плотностью распределения) вероятностей (раздел 3.1.1);

– числовыми (точечными) характеристиками (раздел 3.1.2);

– интервальной характеристикой.

Доверительная погрешность при нормальном распределении:

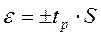(5.3)

В общем случае доверительный интервал для СКО случайной погрешности можно оценить по χ²-распределению (приложение Е):

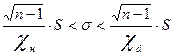(5.4)

где S – выборочное СКО;

χ_н² – значение по χ²-распределению для уровня значимости ,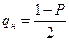

где Р – доверительная вероятность;

χ_в² – значение по χ²- распределению для уровня значимости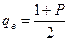

5 СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ

Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Эти погрешности могут быть в большинстве случаев изучены до начала измерений, и результат измерения может быть уточнен или путем внесения поправок, если числовые значения этих погрешностей определены, или путем использования таких способов измерений, которые дают возможность исключить влияние систематических погрешностей без их определения. Результаты измерений тем ближе к истинному значению, чем меньше оставшиеся не исключенные систематические погрешности.

По характеру проявления систематические погрешности подразделяются на постоянные, прогрессивные и периодические (рисунок 2.1).

Постоянные погрешности – погрешности, длительное время сохраняющие свое значение. Они встречаются наиболее часто. К постоянным относятся погрешности большинства мер (гирь, концевых мер длины), погрешности градуировки шкал измерительных приборов и др. Например, погрешность от постороннего груза на чашке весов, погрешность от неточной установки прибора на нуль.

Прогрессивные погрешности – непрерывно возрастающие или убывающие погрешности. К ним относятся погрешности от износа контактирующих деталей средств измерении, постепенное падение напряжения источника тока (аккумуляторных батарей), погрешность от постепенного прогрева измерительной аппаратуры и др.

Периодические погрешности – погрешности, периодически изменяющие значение и знак. Обычно эта погрешность встречается в угломерных приборах с круговой шкалой. Например, погрешность от эксцентриситета круговой шкалы и оси вращения стрелки средства измерений.

Погрешности, изменяющиеся по сложному закону, появляются вследствие действия нескольких систематических погрешностей.

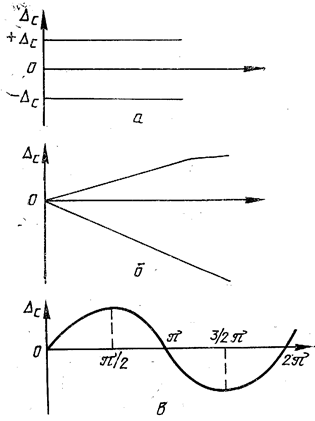
Рисунок 2. – Виды систематических погрешностей:

а) постоянные; б) прогрессивные; в) периодические

Дата добавления: 2014-01-03