IV. Эквивалентное преобразование сопротивления

Эквивалентным называют такое преобразование части схемы, при котором токораспределение в схеме, не подвергнутое преобразованию, остаётся неизменным.

1. Последовательное соединение сопротивлений.

E I

I

Это соединение, при котором ток через любое сопротивление в любой момент времени одинаков.

E = IR₁+ IR₂+...+ IR_n

Мощность, потребляемая цепью не измениться, если все сопротивления заменить их эквивалентными, равными сумме I(R₁+R₂+...+R_n)=IR_э

2. Параллельное соединение сопротивлений.

I

I I I

E R_1` R₂ R_n

По первому закону Кирхгофа: I= I₁+I₂+I₃+...+I_n

Выразим токи данной цепи через параметры схемы:

E/R_э= E/R₁+ E/R₂+...+E/R_n

Параллельное соединение сопротивлений называют такое соединение, при котором напряжение на всех сопротивлениях одинаково.

Следствие из первого з-на Кирхгофа 1/R= 1/R₁+1/R₂+...+1/R_n

Эквивалентная проводимость схемы с параллельными сопротивлениями равна сумме проводимости отдельных параллельных ветвей.

G_э= G₁+G₂+...+G_n где G=1/R

Если параллельно соединены 2 сопротивления, то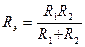

Если параллельно соединены одинаковые по номиналу, то R_э=R/2

3. Преобразование сопротивлений, соединённых треугольником в соединение звездой.

Правило эквивалентных преобразований:

I_1тр=I_1зв

I_2тр=I_2зв

I_3тр=I_3зв

Возьмём и поместим звезду в треугольник, тогда:

Обратное преобразование из звезды в треугольник:

Например:

Ом

Ом

Ом

В результате получили схему:

Ом

Ом

Ом

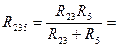2,25 Ом 2,25 Ом

R₁₂₃₄₅=R₁₃₄+R₂₃₅=4,5 Ом

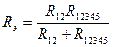
V. Расчёт простых цепей постоянного тока методом эквивалентных преобразований сопротивлений.

Старинное название – метод свёртки схемы.

1. Определяем количество узлов и ветвей в схеме k=2, m=4

2. Сворачиваем схему к одному эквивалентному сопротивлению (эквивалентному)

2.1. Находим в ветвях схемы R, соединённые последовательно, заменяем их эквивалентными и перечерчиваем схему в упрощенном варианте.

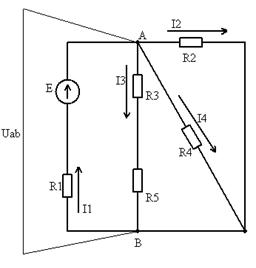R₃₅=R₃+R₅

2.2. Продолжаем свёртку схемы. Находим сопротивления, соединённых параллельно (имеющих пару общих узлов) заменяем их эквивалентными и вновь перечерчиваем схему в упрощённом виде.

Ом

2.3. Продолжаем свёртку схемы, заменяя последовательное и параллельное сопротивление их эквивалентами до тех пор, пока схема не придет к виду: один источник питания и одно эквивалентное сопротивление.

3. По закону Ома определяем ток ветви источника питания

4. Определяем направления на параллельных ветвях. U_AB=I₁R₂₃₄₅

5. По закону Ома для участка цепи определяем токи в параллельных ветвях:

1. Определим мощность, потребляемую цепью. P=I²R_э Вт
2. Баланс мощностей

Дата добавления: 2014-01-03