I. Способы представления переменного синусоидального тока и напряжения

Цепи однофазного переменного тока.

Лекция №4

Вопросы:

1. Способы представления переменного тока
2. Определение схем замещения по заданным векторным диаграммам токов и напряжений. - цепь, содержащая резистор и катушку - цепь, содержащая резистор и конденсатор - цепь, последовательного соединения резистора, конденсатора и катушки
3. Расчёт электрического состояния цепи с последовательным соединением элементов резистор, конденсатор и катушка
4. Расчёт цепи с параллельным соединением элементов R, L, C
5. Мощность цепи синусоидального тока
6. Коэффициент мощности и пути его улучшения

Однофазная цепь – это цепь, к которой подключена одна из фаз нейтрали.

1. Аналитический:

где 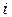– мгновенное значение тока;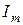– максимальное (амплитудное) значение тока (рис. 2.2); 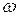– угловая частота; 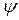– начальная фаза.

2. Символьный: - комплекс - . С математической точки зрения U – модуль вектора или комплекса, с физической точки зрения – это действующее значение напряжения, которое можно измерить вольтметром.

3. Векторная форма

Как известно из математики, синусоидальная функция аргумента определя­ется как проекция радиуса единичной длины на ось ординат, если этот ра­диус поворачивается против часовой стрелки на радиан. Синусоидальному току 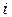соответствует непрерывное вращение радиуса длиной 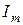с угловой скоростью 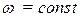против часовой стрелки. Синусоида в координатной плоскости () изображается (рис. 2.4) вращающимся вектором в декартовой системе (). Под углом 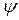, отсчитываемым от положительного направления оси абсцисс , строится вектор . 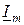Положительные начальные фазы при построении откладывают от оси 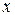против вращения часовой стрелки, отрицательные – по часовой стрелке. Проекция вектора 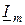на ось у в момент вре­мени 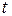= 0 равна мгновенному значению тока 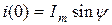. Пусть, начиная с момента 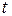= 0, вектор 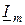вращается вокруг начала координат 0 с постоянной угловой скоростью 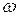в положительном направлении (про­тив движения часовой стрелки). 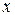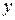К моменту времени вектор повернется относи­тельно оси на угол , и его проекция на ось будет равна мгно­венному значению функции . Таким образом, проекция вращающегося с угловой скоростью 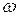вектора 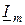на ось ординат в любой момент времени равна мгновен­ному значению синусоидальной функции в этот момент вре­мени.

Рис. 2.4

При представлении синусоидальной функции вращающимся вектором доста­точно изобразить его в координатах только в начальный момент вре­мени (рис. 2.5). Этот вектор 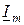представляет или отображает синусоиду, т.е. дает информацию о двух ее параметрах – амплитуде 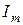и начальной фазе 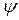. Векторы, изображающие синусоидальные функции, лишены физи­ческого содержания и имеют совсем другой смысл, чем векторы, определяющие модуль и направление физических величин в точке. Задача суммирования (вычитания) синусоид упрощается, если изобразить их векторами на плоскости, и сводится к операции сложения (вычита­ния) векторов, изображающих эти функции. В качестве примера рассмотрим сложение двух токов:

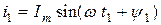и .

На рис.2.5 ток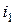и и 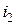изображены в виде векто­ров на плоскости. Вектор, модуль которого равен 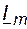, расположенный под углом 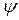к оси 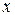, является суммой этих векторов и изображает суммарную синусоиду

При расчетах электрических цепей синусоидального тока обычно оперируют не мгновенными, а дейст­вующими значениями токов и ЭДС. Поэтому складывают не векторы амплитуд, а век­торы действующих значений.

Дата добавления: 2014-01-03