
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция: Эволюционное моделирование и генетические алгоритмы
|
|
|
|
Темы научных исследований и рефератов, интернет-листов
- Математическое моделирование: история, личности, будущее.
- Компьютерное моделирование и его особенности.
- Роль математического моделирования в современном мире.
Рассматриваются основные понятия и принципы эволюционного моделирования систем, а также генетических алгоритмов - адекватного аппарата его проведения.
Цель лекции: ввести в суть проблемы, сформулировать основные положения и принципы, цели эволюционного моделирования и дать общее понятие о генетических алгоритмах и их возможностях в эволюционном моделировании.



Потребность в прогнозе и адекватной оценке последствий осуществляемых человеком мероприятий (особенно негативных) приводит к необходимости моделирования динамики изменения основных параметров системы, динамики взаимодействия открытой системы с его окружением (ресурсы, потенциал, условия, технологии и т.д.), с которым осуществляется обмен ресурсами в условиях враждебных, конкурентных, кооперативных или же безразличных взаимоотношений. Здесь необходимы системный подход, эффективные методы и критерии оценки адекватности моделей, которые направлены не только (не столько) на максимизацию критериев типа "прибыль", "рентабельность", но и на оптимизацию отношений с окружающей средой. Если критерии первого типа важны, например, для кратко- и среднесрочного прогнозирования и тактического администрирования, то второго типа - для средне- и долгосрочного прогноза, для стратегического администрирования. При этом необходимо выделить и изучить достаточно полную и информативную систему параметров исследуемой системы и его окружения, разработать методику введения мер информативности и близости состояний системы. Важно отметить, что при этом некоторые критерии и меры могут часто конфликтовать друг с другом.
Многие такие социально-экономические системы можно описывать с единых позиций, средствами и методами единой теории - эволюционной.
При эволюционном моделировании процесс моделирования сложной социально-экономической системы сводится к созданию модели его эволюции или к поиску допустимых состояний системы, к процедуре (алгоритму) отслеживания множества допустимых состояний (траекторий). При этом актуализируются такие атрибуты биологической эволюционной динамики (в скобках даны возможные социально-экономические интерпретации этих атрибутов для эволюционного моделирования) как, например:
- сообщество (корпорация, корпоративные объекты, субъекты, окружение);
- видовое разнообразие и распределение в экологической нише (типы распределения ресурсов, структура связей в данной корпорации);
- экологическая ниша (сфера влияния и функционирования, эволюции на рынке, в бизнесе);
- рождаемость и смертность (производство и разрушение);
- изменчивость (экономической обстановки, ресурсов);
- конкурентные взаимоотношения (рыночные отношения);
- память (способность к циклам воспроизводства);
- естественный отбор (штрафные и поощрительные меры);
- наследственность (производственные циклы и их предыстория);
- регуляция (инвестиции);
- самоорганизация и стремление системы в процессе эволюции максимизировать контакт с окружением в целях самоорганизации, возврата на траекторию устойчивого развития и другие.
При исследовании эволюции системы необходима ее декомпозиция на подсистемы с целью обеспечения:
- эффективного взаимодействия с окружением;
- оптимального обмена определяющими материальными, энергетическими, информационными, организационными ресурсами с подсистемами;
- эволюционируемости системы в условиях динамической смены и переупорядочивания целей, структурной активности и сложности системы;
- управляемости системы, идентификации управляющей подсистемы и эффективных связей с подсистемами системы, обратной связи.
Пусть имеется некоторая система S с N подсистемами. Для каждой i-й подсистемы определим вектор x(i)=(x1(i),x2(i),:,xni(i)) основных параметров (т.е. параметров, без которых нельзя описать и изучить функционирование подсистемы в соответствии с целями и доступными ресурсами системы) и функцию s(i)=s(x(i)), которую назовем функцией активности или просто активностью этой подсистемы.
Пример. В бизнес-процессах это понятие близко к понятию деловой активности.
Для всей системы определены вектор состояния системы x и активность системы s(x), а также понятие общего потенциала системы.
Пример. Потенциал активности может быть определен аналогично биологическому потенциалу популяции, например, с помощью интеграла от активности на задаваемом временном промежутке моделирования.
Эти функции отражают интенсивность процессов как в подсистемах, так и в системе в целом.
Важными для задач моделирования являются три значения s(i)max, s(i)min, s(i)opt - максимальные, минимальные и оптимальные значения активности i-й подсистемы, а также аналогичные значения для всей системы (smax, smin, sopt). В качестве показателя экономического состояния можно брать также отношение значения этого показателя к его нормированному значению, а для комплексного учета влияния параметров на состояние системы можно использовать аналоги меры информационной близости, например, по К. Шеннону.
Если дана открытая экономическая система (процесс), а Н0, Н1 - энтропия системы в начальном и конечном состояниях процесса, то мера информации определяется как разность вида:
ΔН=Н0-Н1.Уменьшение ΔН свидетельствует о приближении системы к состоянию статического равновесия (при доступных ресурсах), а увеличение - об удалении. Величина ΔН - количество информации, необходимой для перехода от одного уровня организации системы к другой (при ΔН>0 - более высокой, при ΔН<0 - более низкой организации).
Возможен подход и с использованием меры по Н. Моисееву. Пусть дана некоторая управляемая система, о состояниях которой известны лишь некоторые оценки - нижняя smin и верхняя smax. Известна целевая функция управления F(s(t),u(t)), где s(t) - состояние системы в момент времени t, а u(t) - управление из некоторого множества допустимых управлений, причем считаем, что достижимо uopt - некоторое оптимальное управление из пространства U, t0<t<T, smin s
s smax. Мера успешности принятия решения:
smax. Мера успешности принятия решения:
 [t0;T], s
[t0;T], s [smin;smax].
[smin;smax]. Увеличение Н свидетельствует об успешности управления системой (успешности принятого управляющего решения).
Активности подсистем прямо или опосредованно взаимодействуют с помощью системной активности s(x), например, по простой схеме вида
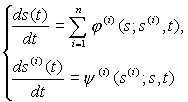
Функции j(i), y(i) должны отражать эволюционируемость системы, в частности, удовлетворять условиям:
- периодичности, цикличности, например:
 0<T<∞,
0<T<∞,  t:
t: 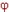 (i)(s; s(i), t)=
(i)(s; s(i), t)=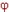 (i)(s; s(i), t+T),
(i)(s; s(i), t+T),  (i)(s; s(i), t)=
(i)(s; s(i), t)= (i)(s; s(i), t+T));
(i)(s; s(i), t+T)); - затухания при снижении активности, например:
 0
0  i=1, 2,..., n) => (
i=1, 2,..., n) => (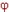 (i)
(i)  0,
0,  (i)
(i)  0);
0); - равновесности и стационарности: выбор (определение) функции
 (i),
(i),  (i) осуществляется таким образом, чтобы система имела точки равновесного состояния, а s(i)opt, sopt достигались в стационарных точках x(i)opt, xopt для малых промежутков времени; в больших промежутках времени система может (в соответствии с теорией катастроф) вести себя хаотично, самопроизвольно порождая регулярные, упорядоченные, циклические взаимодействия (детерминированный хаос).
(i) осуществляется таким образом, чтобы система имела точки равновесного состояния, а s(i)opt, sopt достигались в стационарных точках x(i)opt, xopt для малых промежутков времени; в больших промежутках времени система может (в соответствии с теорией катастроф) вести себя хаотично, самопроизвольно порождая регулярные, упорядоченные, циклические взаимодействия (детерминированный хаос).
Взаимные активности  (ij)(s; s(i), s(j), t) подсистем i и j мы не учитываем. В качестве функции
(ij)(s; s(i), s(j), t) подсистем i и j мы не учитываем. В качестве функции  (i),
(i),  (i) могут быть эффективно использованы производственные функции типа Кобба-Дугласа:
(i) могут быть эффективно использованы производственные функции типа Кобба-Дугласа:
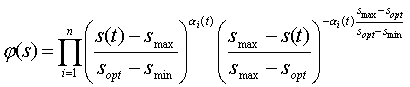
В таких функциях важен параметр  i, отражающий степень саморегуляции, адаптации системы. Как правило, его нужно идентифицировать.
i, отражающий степень саморегуляции, адаптации системы. Как правило, его нужно идентифицировать.
Функционирование системы удовлетворяет на каждом временном интервале (t; t+τ) ограничениям вида
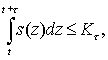
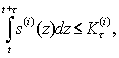
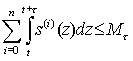
При этом отметим, что выполнение для τ>0 одного из двух условий
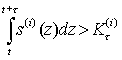
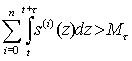
приводит к разрушению (катастрофе) системы.
Пример. Пусть имеется некоторая социально-экономическая среда, которая возобновляет с коэффициентом возобновления  (τ,t,x) (0<t<T, 0<x<1, 0<τ<T) свои ресурсы. Этот коэффициент зависит, в общем случае, от мощности среды (ее ресурсоемкости, ресурсообеспеченности). Рассмотрим простую гипотезу:
(τ,t,x) (0<t<T, 0<x<1, 0<τ<T) свои ресурсы. Этот коэффициент зависит, в общем случае, от мощности среды (ее ресурсоемкости, ресурсообеспеченности). Рассмотрим простую гипотезу:  (τ,t,x)=
(τ,t,x)= 0+
0+ 1x, и чем больше ресурсов - тем больше темп их возобновления. Можно записать непрерывную эволюционную модель (a - коэффициент естественного прироста ресурсов, b - их убыли):
1x, и чем больше ресурсов - тем больше темп их возобновления. Можно записать непрерывную эволюционную модель (a - коэффициент естественного прироста ресурсов, b - их убыли):
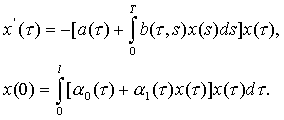
Обозначим  (τ)=
(τ)= 0(τ)+
0(τ)+ 1(τ)x(τ)>0. Тогда
1(τ)x(τ)>0. Тогда
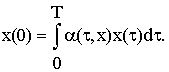
Задача всегда имеет решение x 0. Тогда эволюционный потенциал системы можно определить как величину:
0. Тогда эволюционный потенциал системы можно определить как величину:
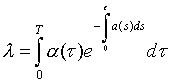
Чем выше темп  - тем выше λ, чем меньше
- тем выше λ, чем меньше  - тем ниже λ. Каким бы хорошим ни было состояние ресурсов в начальный момент, они неизменно будут истощаться, если потенциал системы меньше 1.
- тем ниже λ. Каким бы хорошим ни было состояние ресурсов в начальный момент, они неизменно будут истощаться, если потенциал системы меньше 1.
Пример. Пусть umax - максимальный уровень синтаксических ошибок в программе Р, u(t) - их оставшееся количество к моменту времени t. Исходя из простейшей эволюционной модели du/dt+λumax=0, u(t0)=u0, можно заключить, что уровень ошибок убывает при λ(c-t0) -1 (t0<c<T) по закону: u(t) = u0(1+ λ(c-t))/(1+λ(c-t0)). Если задать дополнительно u(t*)=u*, (umax - неизвестная величина, t*
-1 (t0<c<T) по закону: u(t) = u0(1+ λ(c-t))/(1+λ(c-t0)). Если задать дополнительно u(t*)=u*, (umax - неизвестная величина, t*  t0), то закон изменения уровня ошибок находится однозначно, так как: с=(u* t0 - u0t*)/(λu* - λu0) -1/λ.
t0), то закон изменения уровня ошибок находится однозначно, так как: с=(u* t0 - u0t*)/(λu* - λu0) -1/λ.
Отметим, что если ds/dt - общее изменение энтропии системы при воздействии на систему, ds1/dt - изменение энтропии за счет необратимых изменений структуры, потоков внутри системы (рассматриваемой как открытая система), ds2/dt - изменение энтропии за счет усилий по улучшению обстановки (например, экономической, экологической, социальной), то справедливо уравнение И. Пригожина:
ds/dt = ds1/dt + ds2/dt.При эволюционном моделировании социально-экономических систем полезно использовать и классические математические модели, и неклассические, в частности, учитывающие пространственную структуру системы (например, клеточные автоматы и фракталы), структуру и иерархию подсистем (например, графы и структуры данных), опыт и интуицию (например, эвристические, экспертные процедуры).
Пример. Пусть дана некоторая экологическая система Ω, в которой имеются точки загрязнения (выбросов загрязнителей) xi, i=1, 2,:, n. Каждый загрязнитель xi загрязняет последовательно экосистему в промежутке времени (ti-1; ti], ti=ti-ti-1. Каждый загрязнитель может оказать воздействие на активность другого загрязнителя (например, уменьшить, нейтрализовать или усилить по известному эффекту суммирования воздействия загрязнителей). Силу (меру) такого влияния можно определить через rij, R={rij: i=1,2,:, n-1; j=2,3,:, n}.
Структура задаётся графом: вершины - загрязнители, ребра - меры.
Найдём подстановку минимизирующую функционал вида:
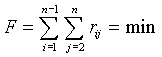
где F - суммарное загрязнение системы с данной структурой S.
Чем быстрее (медленнее) будет произведен учёт загрязнения в точке xi, тем быстрее (медленнее) осуществимы социо-экономические мероприятия по его нейтрализации (усилению воздействия). Чем меньше будет загрязнителей до загрязнителя xi, тем меньше будет загрязнение среды.
В качестве меры rij может быть взята мера, учитывающая как время начала воздействия загрязнителей (предшествующих данной xj), так и число, а также интенсивность этих загрязнителей:
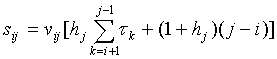
где vij - весовой коэффициент, определяющий степень влияния загрязнителя xi на загрязнитель xj (эффект суммирования), hj - весовой коэффициент, учитывающий удельную интенсивность действия загрязнителя xj или интервал τi, в течение которого уменьшается интенсивность (концентрация) загрязнителя. Весовые коэффициенты устанавливаются экспертно или экспериментально.
Принцип эволюционного моделирования предполагает необходимость и эффективность использования методов и технологии искусственного интеллекта, в частности, экспертных систем.
Основная трудность при построении и использовании эволюционных моделей: в Природе и Познании, в которых эти модели и цели явно или неявно существуют, результаты функционирования системы и достижения цели прослеживаемы часто лишь по прошествии длительного периода времени, хотя в Обществе и Экономике Человек стремится получить результаты в соответствии с целью явно и быстро, с минимальными затратами Ресурсов.
Адекватным средством реализации процедур эволюционного моделирования являются генетические алгоритмы.
Идея генетических алгоритмов "подсмотрена" у систем живой природы, у систем, эволюция которых развертывается в сложных системах достаточно быстро.
Генетический алгоритм - это алгоритм, основанный на имитации генетических процедур развития популяции в соответствии с принципами эволюционной динамики, приведенными выше. Часто используется для решения задач оптимизации (многокритериальной), поиска, управления.
Данные алгоритмы адаптивны, развивают решения, развиваются сами. Особенность этих алгоритмов - их успешное использование при решении NP-сложных проблем (проблем, для которых невозможно построить алгоритм с полиномиально возрастающей алгоритмической сложностью).
Пример. Рассмотрим задачу безусловной целочисленной оптимизации (размещения): найти максимум f(i), i - набор из n нулей и единиц, например, при n=5, i=(1,0,0,1,0). Это очень сложная комбинаторная задача для обычных, "негенетических" алгоритмов. Генетический алгоритм может быть построен следующей укрупненной процедурой:
- генерируем начальную популяцию (набор допустимых решений задачи) - I0=(i1, i2,:, in), ij
 {0,1} и определяем некоторый критерий достижения "хорошего" решения, критерий остановки
{0,1} и определяем некоторый критерий достижения "хорошего" решения, критерий остановки  , процедуру СЕЛЕКЦИЯ, процедуру СКРЕЩИВАНИЕ, процедуру МУТАЦИЯ и процедуру обновления популяции ОБНОВИТЬ;
, процедуру СЕЛЕКЦИЯ, процедуру СКРЕЩИВАНИЕ, процедуру МУТАЦИЯ и процедуру обновления популяции ОБНОВИТЬ; - k:=0, f0:=max{f(i), i
 I0};
I0}; - нц пока не(
 )
) - с помощью вероятностного оператора (селекции) выбираем два допустимых решения (родителей) i1, i2 из выбранной популяции (вызов процедуры СЕЛЕКЦИЯ);
- по этим родителям строим новое решение (вызов процедуры СКРЕЩИВАНИЕ) и получаем новое решение i;
- модифицируем это решение (вызов процедуры МУТАЦИЯ);
- если f0<f(i) то f0:=f(i);
- обновляем популяцию (вызов процедуры ОБНОВИТЬ);
- k:=k+1
кц
Указанные процедуры определяются с использованием аналогичных процедур живой природы (на том уровне знаний о них, что мы имеем). Например, процедура СЕЛЕКЦИЯ может из случайных элементов популяции выбирать элемент с наибольшим значением f(i). Процедура СКРЕЩИВАНИЕ (кроссовер) может по векторам i1, i2 строить вектор i, присваивая с вероятностью 0,5 соответствующую координату каждого из этих векторов-родителей. Это самая простая процедура. Используют и более сложные процедуры, реализующие более полные аналоги генетических механизмов. Процедура МУТАЦИЯ также может быть простой или сложной. Например, простая процедура с задаваемой вероятностью для каждого вектора меняет его координаты на противоположные (0 на 1, и наоборот). Процедура ОБНОВИТЬ заключается в обновлении всех элементов популяции в соответствии с указанными процедурами.
Пример. Работу банка можно моделировать на основе генетических алгоритмов. С их помощью можно выбирать оптимальные банковские проценты (вкладов, кредитов) некоторого банка в условиях конкуренции с тем, чтобы привлечь больше клиентов (средств). Тот банк, который сможет привлечь больше вкладов, клиентов и средств, и выработает более привлекательную стратегию поведения (эволюции) - тот и выживет в условиях естественного отбора. Филиалы такого банка (гены) будут лучше приспосабливаться и укрепляться в экономической нише, а, возможно, и увеличиваться с каждым новым поколением. Каждый филиал банка (индивид популяции) может быть оценен мерой его приспособленности. В основе таких мер могут лежать различные критерии, например, аналог экономического потенциала - рейтинг надежности банка или соотношение привлеченных и собственных средств банка. Такая оценка эквивалентна оценке того, насколько эффективен организм при конкуренции за ресурсы, т.е. его выживаемости, биологическому потенциалу. При этом особи (филиалы) могут приводить к появлению потомства (новых банков, получаемых в результате слияния или распада), сочетающего те или иные (экономические) характеристики родителей. Например, если один банк имел качественную политику кредитования, а другой - эффективную инвестиционную политику, то новый банк может приобрести и то, и другое. Наименее приспособленные особи (филиалы) совсем могут исчезнуть в результате эволюции. Таким образом, отрабатывается генетическая процедура воспроизводства новых банков (нового поколения), более приспособленных и способных к выживанию в процессе эволюции банковской системы. Эта политика со временем пронизывает всю банковскую "популяцию", обеспечивая достижение цели - появления эффективно работающей, надежной и устойчивой банковской системы. Приведем соответствующий генетический алгоритм (укрупненный и упрощенный):
алг ГЕНЕТИЧЕСКИЙ_АЛГОРИТМ_БАНКОВСКОЙ_СИСТЕМЫ ввод Начальная структура банка (начальная популяция); СТРУКТУРА | процедура оценки структуры по приспособлению Стоп:=0 | флаг для завершения эволюционного процесса нц пока (Стоп=0) СЕЛЕКЦИЯ | процедура генетического отбора нового поколения нц пока (МЕРА) | цикл воспроизводства с критерием МЕРА | мерой эффективности банковской системы РОДИТЕЛИ | процедура выбора двух структур (филиалов) | объединяемых (скрещиваемых) на новом шаге ОБЪЕДИНЕНИЕ | процедура образования (объединения) | нового банка (филиала) ОЦЕНКА | процедура оценки устойчивости нового банка, | образования (рейтинга, устойчивости) ВКЛЮЧЕНИЕ | процедура включения (не включения) в новое | поколение (в банковскую систему) кц МУТАЦИЯ | процедура эволюции (мутации) нового поколения если (ПРОЦЕСС) | проверка функционала завершаемости эволюции то Стоп:=1 кцкон.Мы не конкретизируем структуру процедур СЕЛЕКЦИЯ, МЕРА, РОДИТЕЛИ, ОБЪЕДИНЕНИЕ, ОЦЕНКА, ВКЛЮЧЕНИЕ, МУТАЦИЯ, ПРОЦЕСС, хотя даже на интуитивном уровне ясно, что в этом алгоритме они играют решающую роль для эволюционного процесса. Не менее важен и правильный (эффективный) выбор структуры, а также представления (описания) этой структуры. Часто ее выбирают по аналогии со структурой хромосом, например, в виде битовых строк. Каждая строка (хромосома) представляет собой конкатенацию ряда подстрок (генная комбинация). Гены располагаются в различных позициях строки (локусах хромосомы). Они могут принимать некоторые значения (аллели), например, для битового представления - 0 и 1. Структура данных в генетическом алгоритме (генотип) отражает генетическую модель особи. Окружающая среда, окружение определяется вектором в пространстве параметров и соответствует термину "фенотип". Мера качества (процедура МЕРА) структуры часто определяется целевой функцией (приспособленности). Для каждого нового поколения генетический алгоритм осуществляет отбор пропорционально приспособленности (процедура ОТБОР), модификацию (процедуры РОДИТЕЛИ, ОБЪЕДИНЕНИЕ, ВКЛЮЧЕНИЕ) и мутацию (процедура МУТАЦИЯ). Например, в процедуре ОТБОР каждой структуре ставится в соответствие отношение ее приспособленности к суммарной приспособленности популяции и затем происходит отбор (с замещением) всех особей для дальнейшей генетической обработки в соответствии с этой величиной. Размер отбираемой комбинации можно брать пропорциональным приспосабливаемости, и поэтому особи (кластеры) с более высокой приспособленностью с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью. После отбора выбранные особи подвергаются кроссоверу (рекомбинации), т.е. разбиваются на пары. Для каждой пары может применяться кроссовер. Неизмененные особи переходят к стадии мутации. Если кроссовер происходит, полученные потомки заменяют собой родителей и переходят к мутации.
Хотя генетические алгоритмы и могут быть использованы для решения задач, которые, видимо, нельзя решать другими методами, они не гарантируют нахождение оптимального решения (по крайней мере, - за приемлемое время; полиномиальные оценки здесь часто неприменимы). Здесь более уместны критерии типа "достаточно хорошо и достаточно быстро". Главное же преимущество в другом: они позволяют решать сложные задачи, для которых не разработаны пока устойчивые и приемлемые методы, особенно на этапе формализации и структурирования системы, в когнитивных системах. Генетические алгоритмы эффективны в комбинации с другими классическими алгоритмами, эвристическими процедурами, а также в тех случаях, когда о множестве решений есть некоторая дополнительная информация, позволяющая настраивать параметры модели, корректировать критерии отбора, эволюции.
Вопросы для самоконтроля
- Что такое эволюционное моделирование? Каковы критерии эффективности при эволюционном моделировании? Для какого типа прогнозирования (по длительности) используется и является эффективным эволюционное моделирование?
- Что такое генетический алгоритм?
- Каковы основные общие и различные свойства генетических и "не генетических" алгоритмов?
|
|
|
Дата добавления: 2014-01-03; Просмотров: 568; Нарушение авторских прав?; Мы поможем в написании вашей работы!