Плоское движение твердого тела

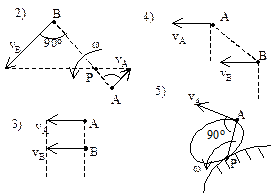
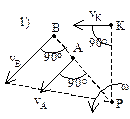
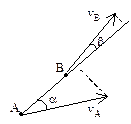
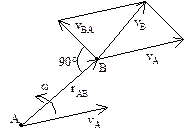Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: x_A= f₁(t), y_A= f₂(t), j = f₃(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят. Скорости точек тела при плоском движении: 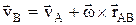; 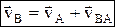, v_BA= w×BA, т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А. Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: v_Acosa = v_Bcosb. Мгновенный центр скоростей – точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если тело движется непоступательно, т.е. w¹0, то мгн.цент.ск. всегда существует. При поступательном движении м.ц.с. находится в ¥. 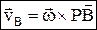– скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена ^ этому отрезку в сторону вращения фигуры. 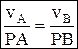, скорости точек тела пропорциональны их расстояниям до м.ц.с. 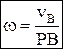, угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с. Определение положения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. v_A и v_B); 3) если они при этом равны между собой, то м.ц.с. находится в ¥, а угловая скорость w=v_A/¥=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в ¥, и угловая скорость w=v_A/¥=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания. Теорема Шаля: плоскую фигуру можно переместить из одного положения в любое другое положение на плоскости одним поворотом этой фигуры вокруг некоторого неподвижного центра. Этот центр на неподвижной плоскости, совпадает с м.ц.с. и называется мгновенным центром вращений (ось вращений). При движении плоской фигуры м.ц.с. непрерывно изменяет свое положение. Геометрическое место м.ц.с., отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место м.ц.с., отмеченных на плоскости фигуры, назыв. подвижной центроидой (колесо катится по прямой: неподвижная центроида – прямая, подвижная – окружность). При движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде (теорема Пуансо).

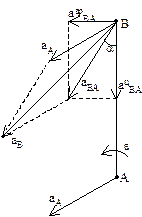Ускорения точек: ,

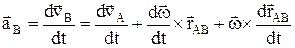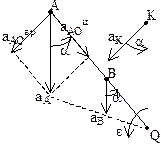
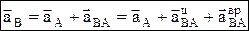– ускорение любой точки (В) фигуры геометрически складывается из ускорения полюса (А) и центростремительного и вращательного ускорений во вращательном движении тела относительно полюса. 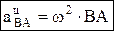, , 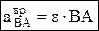, 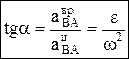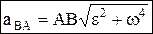. Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом 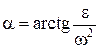к ускорению а_А отрезок 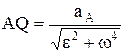, при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол 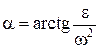: 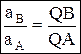. Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.

Дата добавления: 2014-01-03