Динамика твердого тела

Дифференциальные ур-ния поступательного движения твердого тела: 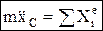и т.д. 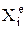– проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 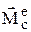0: =0.

Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси: ,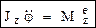

J_z – момент инерции тела относительно оси вращения z, 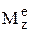– момент внешних сил относительно оси вращения (вращающий момент). 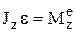_, e – угловое ускорение, чем больше момент инерции при данном 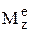_, тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная 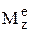_, можно найти закон вращения тела j=f(t), и, наоборот, зная j=f(t), можно найти момент. Частные случаи: 1) если 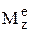= 0, то w = const – тело вращается равномерно; 2) 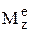= const, то e = const – вращение равнопеременное. Уравнение аналогичное дифф-ному уравнению прямолинейного движения точки .

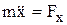Физический маятник – твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Ур-ние вращательного движения:

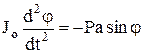, обозначая 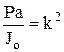, получаем дифф-ное уравнение колебаний маятника: 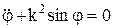, k – частота колебаний маятника. Рассматривая малые колебания, можно считать sinj» j, тогда 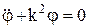– дифф-ное уравнение гармонических колебаний. Решение этого уравнения: j = С₁coskt + C₂ sinkt или j = asin(kt + b), a – амплитуда колебаний маятника, b – начальная фаза колебаний. Период малых колебаний физического маятника Т= 2p/k = 2p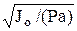. Для малых колебаний маятника период не зависит от угла начального отклонения, этот результат является приближенным. Для математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифф. уравнения движения:

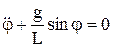, L – длина нити. Если L=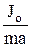, то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L назыв-ся приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, назыв-ся центром качаний физич. маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс.

Дата добавления: 2014-01-03