
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выявление и изучение сезонных колебаний
|
|
|
|
Изучение основной тенденции развития (тренда). Выравнивание рядов динамики. Определение неизвестных значений ряда динамики
Любой ряд динамики может быть представлен виде следующих составляющих:
1) тренд – основная тенденция развития динамического ряда;
2) циклические (периодические) колебания (в том числе сезонные);
3) случайные колебания.
Изучение тренда включает два основных этапа:
- на первом ряд динамики проверяют на наличие тренда;
- на втором производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Существуют следующие методы проверки на наличие тренда в ряду динамики:
1) метод средних – изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из них вычисляется средняя величина; выдвигается гипотеза о существенном различии средних и, если она принимается, признаётся наличие тренда;
2) фазочастотный критерий знаков первой разности (Валлиса и Мура) – ряд имеет тренд, если он не содержит или содержит в приемлемом количестве фазы изменения знака разности первого порядка (абсолютного цепного прироста);
3) критерий Кокса и Стюарта – весь анализируемый ряд динамики разбивается на три равные по числу уровней группы (если количество уровней ряда динамики не делится на три, добавляют недостающие уровни) и сравнивают между собой уровни перовой и последней групп;
4) метод серий – каждый уровень ряда считается принадлежащим одному из двух типов: если уровень ряда меньше медианного значения, то он имеет тип А, в противном случае – тип В; после этого последовательность уровней временного ряда выступает как последовательность типов.
В ходе обработки динамического ряда важнейшей задачей является не только выявление основной тенденции развития явления (тренда), но и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.
Выделяют три основных способа обработки динамического ряда:
а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала;
б) метод скользящей средней;
в) аналитическое выравнивание (выравнивание по аналитическим формулам).
Укрупнение интервалов заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней. По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев рассчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.
Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом (10.20):
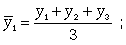
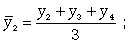
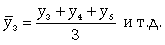 (10.20)
(10.20)
При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая средняя исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так (10.21):
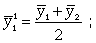
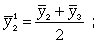
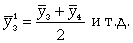 (10.21)
(10.21)
Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.
Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития, его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики, практический анализ - на исследовании линейной диаграммы.
Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:
1) используя полусумму уровней, расположенных рядом с интерполируемыми;
2) по среднему абсолютному приросту;
3) по темпу роста.
Способ определения количественных значений за пределами ряда называют экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем. Экстраполировать можно по средней арифметической, по среднему абсолютному приросту, по среднему темпу роста.
При аналитическом выравнивании может иметь место автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Проверка наличия автокорреляции осуществляется с помощью критерия Дарбина-Уотсона (10.22):
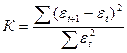 , (10.22)
, (10.22)
где  - отклонение фактического уровня ряда в точке t от теоретического (выравненного) значения.
- отклонение фактического уровня ряда в точке t от теоретического (выравненного) значения.
Если коэффициент автокорреляции равен 0, имеется полная положительная автокорреляция; если коэффициент равен 2, автокорреляция отсутствует; если коэффициент равен 4, наблюдается полная отрицательная автокорреляция.
Прежде чем оценивать взаимосвязь, автокорреляцию необходимо исключить с помощью одного из трёх способов:
1) исключение тренда с авторегрессией (самый эффективный);
2) корреляция первых разностей: от исходных рядов динамики Х и У переходят к новым, построенным по первым разностям;
3) включение фактора времени в уравнение связи.
При использовании второго способа автокорреляцию в рядах можно устранить, коррелируя не сами уровни, а так называемые остаточные величины (разность эмпирических и теоретических уровней). В этом случае корреляцию между остаточными величинами можно определить по формуле (10.23):
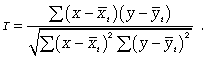 (10.23)
(10.23)
Различают следующие виды зависимостей, используемые при аналитическом выравнивании:
1) линейная форма тренда (10.24):
ye= at + b, (10.24)
где у — уровни, освобожденные от колебаний, выровненные по прямой; b — начальный уровень тренда в момент или период, принятый за начало отсчета времени; а — среднегодовой абсолютный прирост (среднее изменение за единицу времени t; константа тренда).
Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимном погашении особенностей отдельных факторов (ускорение, замедление, нелинейность) часто выражается в примерно постоянной абсолютной скорости изменения, т.е. в прямолинейном тренде.
2) параболическая форма тренда (10.25):
у = а + bt + c t 2, (10.25)
где с — квадратический параметр, равный 1/2 ускорения; константа параболического тренда.
Параболический тренд выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного (регрессивного) развития.
3) экспоненциальная форма тренда (10.26, 10.27, 10.28):
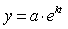 , у = exp (a0 + a1*t), у = exp (a0 + a1*t + a2 t 2), (10.26, 10.27, 10.28)
, у = exp (a0 + a1*t), у = exp (a0 + a1*t + a2 t 2), (10.26, 10.27, 10.28)
где k — темп изменения в разах; e — константа тренда.
Если k > 1, экспоненциальный тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. При k <1 экспоненциальный тренд означает тенденцию постоянно все более замедляющегося роста уровней динамического ряда.
4) логарифмическая форма тренда (10.29):
y = а + b lg(t). (10.29)
Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельного возможного значения.
Для определения параметров уравнения тренда применяют метод избранных точек, метод наименьших расстояний и метод наименьших квадратов (МНК). Применение МНК для определения параметров линейного тренда y e = at + b дает систему двух линейных уравнений, решение которой выбирается таким образом, чтобы Σt = 0. В рядах с нечетным числом членов это выполняется при условии, что для центрального члена ряда t = 0 и вправо t — +1, +2, +3..., а влево: -1, -2, -3...
Во многих случаях, когда в рядах динамики наблюдаются явно выраженные периодические колебания, для описания тренда следует использовать спектральный анализ, когда динамический ряд аппроксимируется функциями Фурье. Расчет спектральной функции осуществляется в следующем порядке:
1) разложение динамики показателя в ряд Фурье;
2) определение значений интенсивности спектрограммы;
3) расчет значений спектральной функции с помощью сглаживания с интервалом усреднения;
4) для анализа связи между отдельными уровнями ряда строят автокорреляционные функции.
Наибольшую точность при прогнозировании нестационарных временных рядов в экономике дают модели, совмещающие процессы выделения тренда и учитывающие при этом процессы автокорреляции. Это так называемые модели авторегрессии — проинтегрированного скользящего среднего ARIMA (аббревиатура от англ. — AutoRegressive Integrated Moving Average). Среди этого класса моделей доминирует модель Бокса—Дженкинса.
При анализе рядов динамики необходимо принимать во внимание, что в зависимости от расстояния между уровнями ряды динамики подразделяются на ряды динамики с равностоящими и неравностоящими уровнями во времени. В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные. Если математическое ожидание значения признака и дисперсия постоянны, не зависят от времени, процесс считается стационарным и ряды динамики также называются стационарными. Экономические и социальные процессы во времени обычно не являются стационарными, т.к. содержат основную тенденцию развития, но их можно преобразовать в стационарные путем исключения тенденций.
Анализ рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития:
1) гармонический анализ – выполняют, представляя временной ряд как совокупность гармонических колебательных процессов; аппарат гармонического анализа позволяет оценить роль каждого колебательного процесса в общей дисперсии временного ряда;
2) индексы сезонности – показывают, во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции f(t); представляют собой относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции.
При относительно неизменном годовом уровне явления (тренд отсутствует либо незначителен) индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период (10.30):
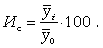 (10.30)
(10.30)
В условиях изменчивости годового уровня (при наличии тренда) индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев (10.31):
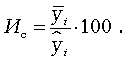 (10.31).
(10.31).
Т. о., в общем случае в ряду динамики можно выделить его четыре основные компоненты:
1) основная тенденция (тренд) (Т);
2) циклическая или конъюнктурная (К);
3) сезонная (S);
4) случайные колебания (E).
Если ряд динамики разбить на различные компоненты, то функция, его описывающая, будет иметь вид (10.32):
Y = f (T, K, S, E). (10.32)
В зависимости от взаимосвязи компонентов между собой может быть построена аддитивная или мультипликативная модель ряда.
Аддитивная модель ряда динамики имеет вид (10.33):
Y = T + K + S + E. (10.33)
и характеризуется тем, что циклические и сезонные колебания остаются постоянными.
Мультипликативная модель ряда имеет вид (10.34):
Y = T × K × S × E. (10.34)
В этой модели характер циклических и сезонных колебаний остается постоянным только по отношению к тренду.
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1821; Нарушение авторских прав?; Мы поможем в написании вашей работы!