Уравнения движения трехфазной фильтрации

Уравнения движения I-фазы – фильтрации – можно описать законом Дарси, записанным для каждой фазы

(6.3)

I=1,2,3

где v_i – скорость фильтрации I-фазы;

k –абсолютная проницаемость;

- относительная проницаемость I- фазы;

- динамическая вязкость I- фазы;

P_i- пластовое давление I-фазы;

- плотность I-фазы.

Давления в фазах вообще говоря не равны между собой и отличаются на величину капиллярного давления.

(6.4)

где P_k – капиллярное давление или капиллярный скачок.

Из курса физики пласта известно, что

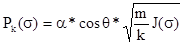(6.5)

где 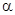- коэффициент поверхностного натяжения;

- статический краевой угол смачивания между жидкостями и породой;

m- пористость;

- безразмерная функция Леверетта, которая определяется для каждого типа коллектора.

6.3 Уравнения неразрывности трех- и двухфазной фильтрации.

Из курса Механики сплошной среды известно, что уравнения неразрывности (сплошности) можно представить в виде

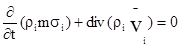I=1,2,3 (6.6)

Обозначения те же.

Для слабосжимаемых или несжимаемых жидкостей, в случае двухфазной фильтрации, имеем

I=1,2 (6.7)

Для непоршневого вытеснения нефти водой, учитывая что , уравнения (6.7) примут вид

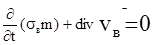
(6.8)

Наиболее разработаны модели одномерного движения двухфазных жидкостей – прямолинейно-параллельное и плоскорадиальное течения.

Одномерные модели предполагают следующие допущения:

- жидкости несжимаемые и несмешиваемые;

- фазовые переходы отсутствуют;

- динамические вязкости -постоянны;

- относительные проницаемости и капиллярное давления являются известными функциями водонасыщенности;

- пористая среда несжимаема m- const.

при этих предположениях, полагая из (6.8) получим

(6.9)

Суммируя уравнения (6.9), получим

(6.10)

Поскольку , из (6.10) следует, что суммарная скорость фильтрации двух фаз не зависит от координат, а зависит только от времени

v(t)=v_в(t)+v_н(t) (6.11)

Из (6.11) следует, что суммарный объемный расход для прямолинейно-параллельного потока также зависит только от времени или может быть постоянным:

Q(t)=v(t)Bh (6.12)

где B,h – ширина и толщина галереи(пласта)

Для плоскорадиального потока объемный расход(дебит) зависит от времени и от r –расстояния до оси скважины;

Q(t)=v(t)2rh (6.13)

Полная система уравнений для описания двухфазной фильтрации состоит из 4-х уравнений движения (6.3), двух уравнений неразрывности (6.9), которые дополняются уравнениями состояния или реологическими уравнениями, начальными и граничными условиями.

Дата добавления: 2014-01-03