
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные законы движения воздуха в шахтной вентиляционной сети
|
|
|
|
Движение воздуха по шахтным вентиляционным сетям подчиняется законам сохранения массы и энергии.
Согласно закону сохранения массы, сумма масс воздуха, подходящих к узлу в единицу времени, должна быть равна сумме масс, уходящих от узла в единицу времени. Поскольку удельный вес воздуха в пределах узла практически не меняется, вместо масс можно оперировать расходами воздуха Q. Для приведенной на рис.6.3 схемы имеем
 |
Рис.6.3 Узел вентиляционной сети
Q1+Q2=Q3+Q4 (6.3)
или
Q1+Q2+Q3+Q4 =0 (6.4)
В общем виде
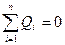 (6.5)
(6.5)
где n-число ветвей соединяющихся в узле;
i- номер подходящей к узлу ветви.
Соотношение (6.5) является математическим выражением первого закона сетей.
Рассмотрим изменение энергии, в каком либо элементарном контуре, например 1-2-3-4-5-1 на рис.6.4. Совершим полный его обход по часовой стрелке от узла 1. Вследствие однозначности давления в любой точке сети общее падение давления на пути 1-2-3-4-5-1 будет равно нулю
 | |||
 | |||
Рис.4.4 Элементарный контур вентиляционной сети
ΔР1-2-3-4-5-1=0 (6.6)
Учитывая, что на пути 1-2-3-4 давление падает, так как направление обхода совпадает с направлением движения воздуха, а на пути 4-5-1 взрастает, так как направление обхода противоположно направлению движения, будем иметь
ΔР1-2-3-4=ΔР4-5-1 (6.7)
Но
ΔР1-2-3-4=ΔР1-2+ΔР2-3+ΔР3-4=h1-2+h2-3+h3-4;
ΔР4-5-1=ΔР4-5+ΔР5-1=h4-5+h5-1;
где h-депрессия соответствующей ветви.
Следовательно, согласно соотношению (6.7) можно записать
h1-2+h2-3+h3-4=h4-5+h5-1
Поскольку h>0, если направление воздуха в ветви совпадает с направлением обхода, и h<0, если эти направления противоположны, имеем в общем, виде
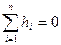 (6.8).
(6.8).
Равенство (6.8) выражает второй закон сетей или закон сохранения энергии в сети. Это равенство действительно для случая, когда в контуре нет источника энергии.
|
|
|
Если в контуре один или несколько источников энергии (вентилятор, естественная тяга и др. (рис.6.4)), то суммарная потеря энергии в контуре будет равна, энергии, поступающей от этих источников
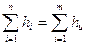 (6.9).
(6.9).
Равенство (6.9) выражает второй закон сетей для случая, когда в контуре имеется источник энергии.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 465; Нарушение авторских прав?; Мы поможем в написании вашей работы!