Формирование первого сценария

Пример 3.

Метод сценариев.

Предположим, что по результатам анализа проекта примера 2 были составлены следующие сценарии его развития и определены возможные вероятности их осуществления. Провести анализ собственного риска проекта.

Расчет NCF и NPV, исходя из исходных данных ячеек D3:D12 (наиболее вероятные значения):

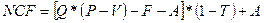
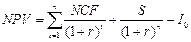или ПЗ(r;n;-NCF)+ПЗ(r;n;0;-S)-I₀

Исходные данные по проекту производства продукта "А"
Показатели	Текущие значения	Сценарий наихудший Р=0,25	Сценарий наилучший Р=0,25	Сценарий вероятный Р=0,5
Объем выпуска Q
Цена за штуку P
Переменные затрат V
Норма дисконта r	10%	15%	8%	10%
Срок проекта n
Постоянные затраты F
Амортизация А
Налог на прибыль Т	60%
Остаточная стоимость S
Начальные инвестиции I0
Чистые платежи (NCFt)	1 460,00р.
Значения (NPVt)	3 658,73р.	4 149,40р.	3 965,47р.	3 658,73р.

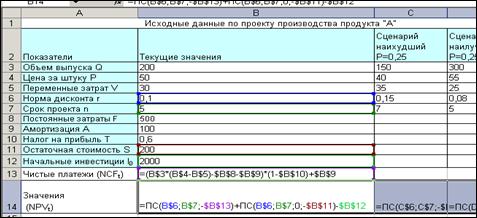
1.1. Выделить блок ячеек, которые будут использоваться в качестве изменяемых (блок В3:В7).

1.2. Выбрать Сервис - Сценарии - Диспетчер сценариев – Добавить.

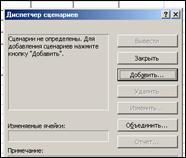
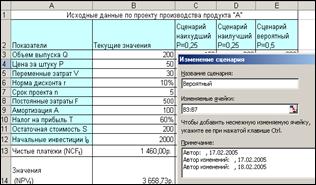
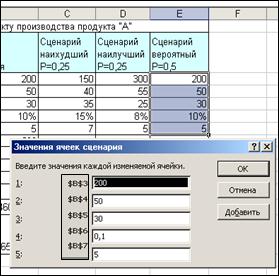
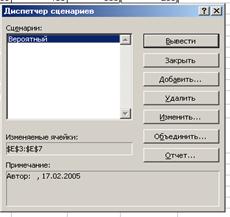
1.3. Введите имя сценария (Вероятный).

1.4. Самостоятельно задайте для сценариев «Наилучший» и «Наихудший» адреса изменяемых ячеек (блок В3:В7) и введите для новых сценариев соответствующие значения.

Наилучший: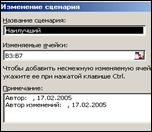

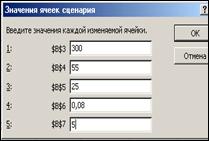
Наихудший: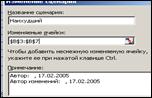

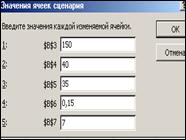
1.5. Нажмите кнопку: Отчет – тип отчета - Структура. Ячейка результатов – B14. далее автоматически будет сформирован отчет на отдельном листе рабочей книги.

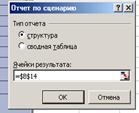
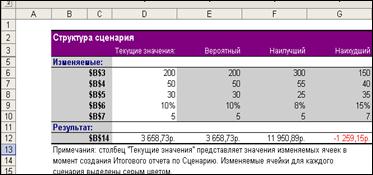
Как следует из структуры сценария, чистая приведенная стоимость проекта при наиболее неблагоприятном развитии событий будет NPV<0 (-1259,15 р.). При нормальном (ожидаемом) или наиболее благоприятном развитии событий проект обеспечивает получение положительной NPV (3658,73 р. и 11950,89 р.).

2. Проведем оценку вероятностного распределения значений критерия NPV.

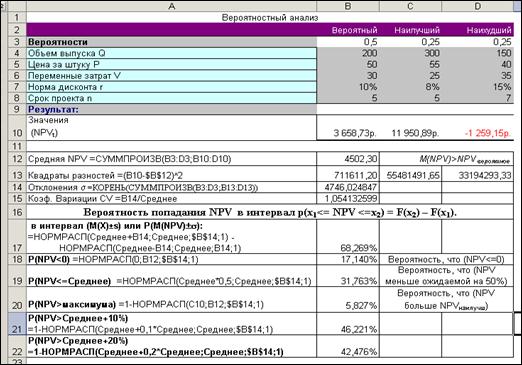
2.1. Скопируем лист «Структура сценария», назвав копию «Анализ рисков», и изменим его.

2.2. Определим среднее ожидаемое значение NPV (ячейка B12): 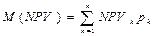или = СУММПРОИЗВ(B3:D3;B10:D10) = 4502,30.

Заметим, что среднее ожидаемое значение больше вероятного значения:

(M(NPV) = 4502,3)>(NPV_вероят =3658,73),

2.3. Для вычисления стандартного отклонения :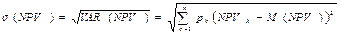

2.3.1. предварительно определим квадраты разностей между средней ожидаемой NPV и множеством ее полученных значений (ячейка B13)

=(B10-$B$12)^2 = 711611,20.

2.3.2. Вычислим квадратный корень из дисперсии (ячейка B14) = КОРЕНЬ(СУММПРОИЗВ(B3:D3;B13:D13)) = 4746,02

Заметим, что среднее ожидаемое значение меньше стандартного отклонения:

(M(NPV) = 4502,3)<(s(NPV) = 4746.02)

2.4. Определим коэффициент вариации 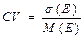(ячейка B15) =B14/В12 = 1,054.

Значение коэффициента вариации CV>1, следовательно, риск данного проекта на среднюю единицу дохода несколько выше.

2.5. Исходяиз соотношения р(x₁<= Е <=x₂) = F(x₂) – F(x₁) определим вероятность того, что NPV попадет в интервал в интервал (М(Х)± s), т.е. определим P(M(NPV)±s) (ячейка В17): F(x₂) – F(x₁) = F(М(Х)+ s) – F(М(Х) - s) или

=НОРМРАСП(М(NPV)+ s; М(NPV); s;1) - НОРМРАСП(М(NPV) -s; М(NPV); s;1) или

=НОРМРАСП(B12+B14; B12;B14;1)-НОРМРАСП(B12-B14; B12;B14;1) = 68,3%

Исходя из предположения о нормальном распределении случайной величины, с вероятностью около 70% можно утверждать, что значение NPV будет находиться в диапазоне 4502,03±4673,62.

2.6. Определим вероятность того, что NPV будет иметь нулевое или отрицательное значение, p(NPV)<=0): (ячейка В18) =НОРМРАСП(0;B12;$B$14;1)=17.4%.

Существует приблизительно один шанс из шести возникновения убытков.

2.7. Определим вероятность того, что NPV будет меньше ожидаемой М(NPV) на 50%, P(NPV<= 0,5*M(NPV)) - ячейка В19:

=НОРМРАСП(B12 *0,5; B12;B14;1) = 32%.

2.8. Определим вероятность того, что NPV будет больше NPV_{наилучшего},

P(NPV> NPV_{наилучшего}) ) - ячейка В20:

=1-НОРМРАСП(С10;B12;$B$14;1)=5.8%

2.9. Определим вероятность того, что NPV будет больше ожидаемой М(NPV) на 10%, P(NPV> 1,1*M(NPV)) ) - ячейка В21:

=1-НОРМРАСП(1,1*Среднее;Среднее;$B$14;1) = 46%

2.10. Определим вероятность того, что NPV будет больше ожидаемой М(NPV) на 20%, P(NPV> 1,2*M(NPV)) ) - ячейка В22:

=1-НОРМРАСП(1,2*Среднее;Среднее;$B$14;1) = 43%

Полученные результаты анализа показывают наличие риска для данного проекта. Несмотря на то, что среднее значение превышает прогноз экспертов

M(NPV) = 4502,3>NPV_вероят =(3658,73), ее величина меньше стандартного отклонения.

M(NPV) = 4502,3<s(NPV) = 4746.02

3. Самостоятельно определите вероятности того, что:

3.1. величина NPV будет меньше 70% от ожидаемой средней;

3.2. величина NPV будет больше ожидаемой средней на величину двух стандартных отклонений.

3.3. Объясните полученные результаты.

Дата добавления: 2014-01-03