Исследование функций и построение графиков. При построении графиков функций полезно придерживаться следующего плана:

При построении графиков функций полезно придерживаться следующего плана:

1. Находят область определения функции и определяют точки разрыва, если они имеются.

2. Устанавливают, является функция четной или нечетной или ни той ни другой. Если функция четна или нечетна, то достаточно рассмотреть ее значения при x>0, а затем симметрично относительно оси OY или начала координат восстановить ее и для значений x<0.

3. Исследуют функцию на периодичность. Если функция периодическая, то достаточно рассмотреть ее на одном периоде.

4. Находят точки пересечения графика функции с осями координат (если это возможно)

5. Проводят исследование функции на экстремум и находят интервалы возрастания и убывания функции.

6. Находят точки перегиба кривой и интервалы выпуклости, вогнутости функции.

7. Находят асимптоты графика функции.

8. Пользуясь результатами шагов 1-7, строят график функции. Иногда для большей точности находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой.

Пример. Исследовать функцию y=x³-3x и построить график.

1) Функция определена на интервале (-∞; +∞). Точек разрыва нет.

2) Функция является нечетной, т.к. f(-x) = -x³-3(-x) = -x³+3x = -f(x), следовательно, она симметрична относительно начала координат.

3) Функция не периодическая.

4) Точки пересечения графика с осями координат: x³-3x=0, х = 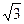, х = -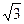, х = 0, т.е. график функции пересекает оси координат в точках: (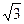; 0), (0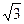; 0), (- ; 0).

5) Найдем точки возможного экстремума: у′ = 3х²-3; 3х²-3=0; х = -1; х = 1.Область определения функции разделится на промежутки: (-∞; -1), (-1; 1), (1; +∞). Найдем знаки производной в каждом получившемся промежутке:

- на интервале (-∞; -1) у′>0 – функция возрастает

- на интервале (-1; 1) у′<0 – функция убывает

- на интервале (1; +∞) у′>0 – функция возрастает. Точка х = -1 – точка максимума; х = 1 – точка минимума.

6) Найдем точки перегиба: у′′ = 6х; 6х = 0; х = 0. Точка х = 0 разбивает область определения на промежутки (-∞; 0), (0; +∞). Найдем знаки второй производной в каждом получившемся промежутке:

- на интервале (-∞;0) у′′<0 – функция выпуклая

- на интервале (0; +∞) у′′>0 – функция вогнутая. х = 0 – точка перегиба.

7) Асимптот у графика нет

8) Построим график функции:

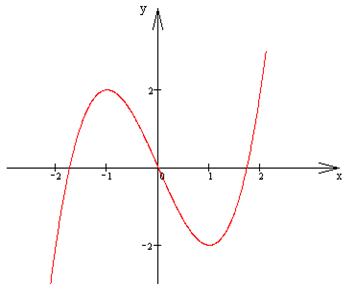
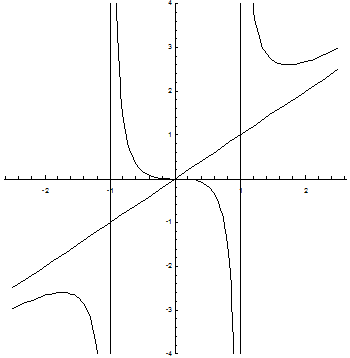
Пример. Исследовать функцию 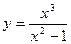и построить ее график.

1) Областью определения функции являются промежутки (-¥; -1) È (-1; 1) È (1; ¥). Областью значений данной функции является интервал (-¥; ¥).

Точками разрыва функции являются точки х = 1, х = -1.

2) Функция является нечетной, т.к. .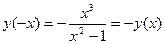

3) Функция не периодическая.

4) График пересекает оси координат в точке (0; 0).

5) Находим критические точки.

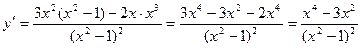
Критические точки: x = 0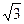; x = -; x = 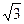; x = -1; x = 1.

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

-¥ < x < -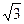, y¢ > 0, функция возрастает

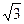-< x < -1, y ¢ < 0, функция убывает

-1 < x < 0, y ¢ < 0, функция убывает

0 < x < 1, y ¢ < 0, функция убывает

1 < x < 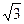, y ¢ < 0, функция убывает

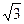< x < ¥, y ¢ > 0, функция возрастает

Видно, что точка х = -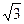является точкой максимума, а точка х = 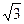является точкой минимума. Значения функции в этих точках равны соответственно 3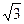/2 и -3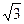/2.

6) Найдем вторую производную функции

.

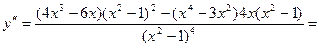
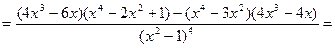
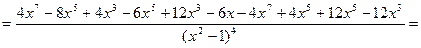
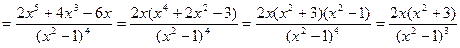Определим выпуклость и вогнутость кривой на промежутках.

-¥ < x < -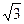, y ¢¢ < 0, кривая выпуклая

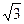-< x < -1, y ¢¢ < 0, кривая выпуклая

-1 < x < 0, y ¢¢ > 0, кривая вогнутая

0 < x < 1, y ¢¢ < 0, кривая выпуклая

1 < x < 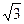, y ¢¢ > 0, кривая вогнутая

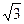< x < ¥, y ¢¢ > 0, кривая вогнутая

7) Найдем асимптоты кривой. Прямые х = 1, х = -1 являются вертикальными асимптотами, т.к. в них односторонние пределы равны бесконечности. Теперь найдем наклонные асимптоты.

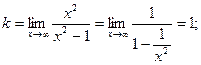
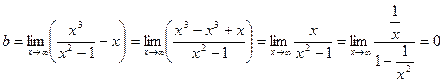
Уравнение наклонной асимптоты: y = x.

8) Построим график функции:

Дата добавления: 2014-01-03