Несобственные интегралы

Понятие определенного интеграла вводилось и изучалось, во-первых, в предположении, что интегрируемая функция должна быть ограниченной на отрезке интегрирования, во-вторых, сам отрезок должен быть конечным. Если хотя бы одно из этих необходимых требований не выполнено, то определенный интеграл не существует.

Оказывается, существуют классы функций, для которых, хотя и нарушены указанные требования, можно говорить о существовании определенного интеграла. Естественно, при этом определенный интеграл понимается не в обычном смысле, а рассматривается некоторое его обобщение. Укажем два основных класса таких функций.

1. Несобственные интегралы первого рода.

Пусть функция f(x) определена и непрерывна на промежутке [ a, ¥). Тогда она непрерывна на любом отрезке [ a, b ].

Если существует конечный предел 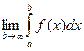, то этот предел называется несобственным интегралом1-го рода от функции f(x) на промежутке [ a, ¥).

Обозначается: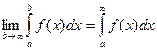

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

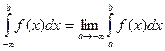
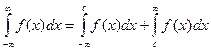
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Пример. 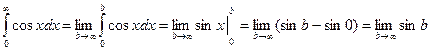- не существует, следовательно, несобственный интеграл расходится.

Пример. 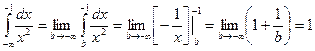- интеграл сходится

Теорема: Если для всех х (x ³ a) выполняется условие 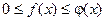и интеграл 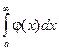сходится, то 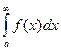тоже сходится и 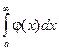³ .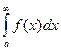

Теорема: Если для всех х (x ³ a) выполняется условие 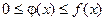и интеграл 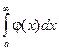расходится, то 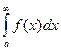тоже расходится.

Теорема: Если 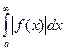сходится, то сходится и интеграл .

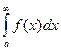В этом случае интеграл 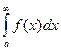называется абсолютно сходящимся.

Пример. Рассмотрим несобственный интеграл 1-го рода функции 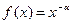на промежутке 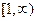. При 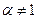имеем:

.

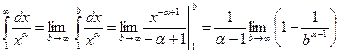Отсюда следует, что при 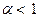несобственный интеграл расходится, а при 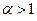он сходится, причем , .

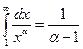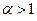Легко убедиться, что рассматриваемый несобственный интеграл расходится и при .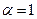

2. Несобственные интегралы второго рода.

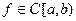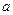Пусть , где и 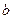– некоторые числа, причем 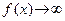при (функция неограничена). Тогда .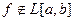

Возьмем 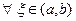. Тогда 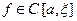и, следовательно, .

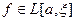Несобственным интегралом 2-го рода функции 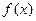на промежутке 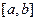называют предел .

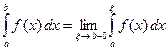Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.

Так же, как и выше, определяют интеграл от функции, неограниченной в окрестности точки .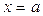

Пример. Исследовать на сходимость несобственный интеграл 2-го рода функции 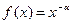, , 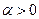на промежутке 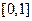. При 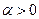, 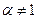имеем:

.

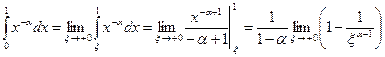Из полученных соотношений следует, что если 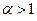, то несобственный интеграл расходится; если же 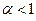, то сходится, причем , .

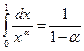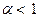Рассматриваемый несобственный интеграл расходится и при .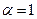

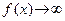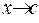Наконец, если при , где 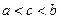, то полагают

.

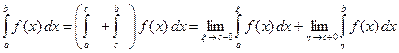Дата добавления: 2014-01-03