Предикаты. Операции над предикатами

Основные понятия. В исчислении высказываний изучались логические отношения, составленные из простых высказываний и принимающие только два значения 0 или 1 с помощью операций конъюнкция, дизъюнкция, отрицание (инверсия), импликация, эквиваленция. Однако для задания более сложных логических рассуждений исчисления высказываний недостаточно.

На практике используются заключения, зависящие как от структуры, так и от содержания используемых в них высказываний. В некоторых случаях высказывания касаются свойств объекта или отношений между объектами. Поэтому следует расширить логику высказываний и построить такую логическую систему, в рамках которой можно было бы исследовать структуру и содержание тех высказываний, которые в рамках алгебры высказываний считались бы элементарными.

Такой логической системой является логика предикатов, а алгебра высказываний – ее составной частью.

Предикат (от лат. «сказуемое») - повествовательное предложение, содержащее предметные переменные, определённые на соответствующих множествах. При замене переменных конкретными значениями (элементами множеств) предикат обращается в высказывание, т.е. принимает значение истина или ложь. Обозначение предиката:

P(x₁,x₂…x_m), x₁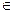M₁,… x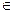_mM_m.

У каждой предметной переменной своя область определения. Можно дать иное определение предиката.

Одноместным предикатом P(x) называется произвольная функция переменного x, определенная на множестве М и принимающая значения из множества {0,1}

Множество М, на котором определен предикат P(x), называется предметной областью или областью определения предиката. Множество всех x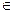M, при которых P(x)=1, называется множеством истинности предиката

P(x): J_p={x | x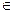M, P(x)=1}

Предикат P(x), определенный на множестве М, называется тождественно истинным, если J_p=M, и тождественно ложным, если J_p=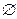,. Если для булевой функции область значений функции и область изменения аргумента по типу одна и та же: логическая {0,1}, то для предикатов область значений функции – логическая, а область изменений аргументов – предметная.

N-местным предикатом называется всякая функция n переменных P(x₁,x₂,..,x_n), определенная на множестве М=М₁М₂...М_n (декартово произведение) и принимающая на этом множестве одно из двух значений “истина” или “ложь”

Иными словами n – местный предикат P(x₁,x₂,…,x_n) есть отображение n-ой степени произвольного множества в бинарное множество В, элементы которого принимают значения «истина» или «ложь».

P: MB, где М – произвольное множество, а В={0,1}

Пример 1. а) Студент x выполнил лабораторную работу по физике – одноместный предикат. Студент x выполнил лабораторную работу по предемеу y – двухместный предикат.

Если в одноместном предикате вместо переменной x поставить фамилию студента, то получается высказывание.

б) Луна – спутник Венеры – ложное высказывание, не являющееся предикатом, т.к. в нем нет аргумента – переменного х.

в) - то же самое.

г) x²+3x+2=0 – предикат. Здесь xM=R, I_p={-2,-1}.

Независимое высказывание можно рассматривать как нульместный предикат.

Свойство – одноместный предикат,

n- местное отношение – n-местный предикат.

Предикат на конечных множествах может быть задан соответствующей таблицей (таблица 1).

Пример 2. На множестве М_XМ_Y задан предикат Р(x,y) «x<y». М_X= {1,2,3}, М_Y={2,4,5}.

Таблица 1

В ячейках таблицы указано истинностное значение предиката Р(x) в зависимости от условий. Так, в ячейке (1,2) выполняется условие предиката «x<y» (1<2), поэтому Р(x,y)=1. В ячейке (3,2) это условие не выполняется (3 не меньше 2), поэтому Р(x,y) =0. Если незначительно изменить предикат Р(x,y)(знак < изменить на ): изменится значение Р(x,y) в ячейке (2,2). В ней будет стоять не 0, а 1, т.к. 2=2.

Дата добавления: 2014-01-03