Пример 4

а) x – кошка, P(x) – у x есть усы. Усы есть у всех кошек 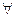xP(x).

Найдется кошка без усов 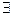x .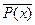

Не бывает кошек с усам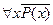и; или ;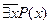

б) x – человек, P(x) – x высокий, Q(x) – x толстый

Любой человек высокий и толстый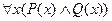

Найдется некто короткий и толстый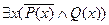

Нет никого высокого и худого ,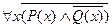

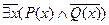
Найдется некто короткий и худой ,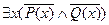

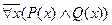
Таким образом, отрицанием предиката P(x) называется новый предикат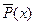, который принимает значение “истина” при всех значениях 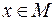, при которых P(x) принимает значения “ложь” и наоборот. Здесь очевидно, I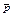=M\I_p.

Конъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x)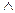Q(x), который принимает значения “истина“ только при тех значениях x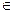М, при которых каждый из предикатов принимает значения “истина“, и “ложь“ во всех остальных случаях. Область определения истинности предиката P(x)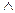Q(x) – это J_p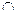J_Q.

Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x)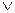Q(x), который принимает значения “ложь” при тех и только тех значениях 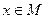, при которых каждый из предикатов принимает значения “ложь”, и принимает значение “истина” во всех остальных случаях. Ясно, что I_Q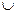I_P.

Импликацией P(x) и Q(x) называется новый предикат 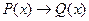, который является ложным при тех и только тех значениях 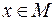, при которых одновременно P(x) принимает значения “истина”, а Q(x) – значение ложь, и принимает истинное значение во всех остальных случаях.

Эквиваленцией предикатов P(x) и Q(x) будет предикат 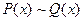, который принимает значение «истина» только тогда, когда P(x) и Q(x) принимают одинаковые значения. Эти же правила справедливы и в случае, если рассматриваются не только одноместные предикаты.

Пример 5. На множестве М={3,4,5,6,7,8} заданы два предиката P(x): “x – простое число“, Q(x): “x – нечетное число“. Составить их таблицы истинности. Равносильны ли предикаты P(x) и Q(x) на множествах L={2,3,4,5,6,7,8}, К={3,4,5,6,7,8,9}?

Таблица 2

М
P(x)
Q(x)

Очевидно, что Ip={3,5,7}, Iq={3,5,7}. Таким образом, на множестве М P(x)=Q(x). На L и K предикаты не равносильны, ибо на множестве L, например, 2- число простое и четное, а на множестве К - число 9 – нечетное, но составное число.

РАЗДЕЛ 4. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ

Дата добавления: 2014-01-03