Распространение выборочных результатов

Распространение выборочных оценок на генеральную совокупность состоит в определении характеристик генеральной совокупности на основе характеристик выборочной. Применяются два способа распространения выборочных данных:

1) способ прямого пересчета;

2) способ поправочных коэффициентов.

При первом способе средние величины и доли, полученные в результате исследования выборочной совокупности, переносятся на генеральную. Если известна численность генеральной совокупности, то можно оценить общий объем признака и возможные интервалы этого объема.

Например, если средняя выборочная урожайность на n =10 га зерновых культур равна 20 ц/га, а предельная ошибка урожайности (ошибка выборки) Δ =2,5 ц/га, то при известной посевной площади в N =2000 га можно установить ожидаемый объем валового сбора –

ВС = 20·2000 = 40000 ц.

Пределы возможного валового сбора оцениваются по величине дисперсии этого показателя. Допустим, что предельная ошибка выборки была оценена при доверительной вероятности равной 0,954 т.е. t =2. Тогда, используя формулу предельной ошибки выборки, 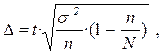заключаем, что выборочная дисперсия показателя урожайности 1 га была

.

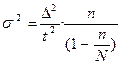Или 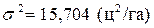. Таким образом, дисперсия возможного валового сбора оценивается как 15,704·2000=31407 ц².(Здесь использовано, то положение, что дисперсия суммы независимых случайных величин равна сумме дисперсий каждой случайной величины) Среднее квадратическое отклонение для всего валового сбора составляет

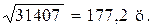
Следовательно, с вероятностью 0,997 (т.е. практически всегда) валовой сбор со всей площади ожидается в пределах 40000 ц. плюс-минус 3 средних квадратических отклонения, т.е. от 40000-532=39,5 тыс.ц до 40000+532=40,5 тыс. ц..

Второй способ используется для уточнения данных сплошного наблюдения. Так, если выборочное наблюдение показало, что недоучет величины исследуемого явления составил 0,5 %, то эту последнюю величину (поправочный коэффициент) распространяют на результат, полученный при сплошном наблюдении, путем увеличения его на 0,5 %.

Контрольные вопросы

1. Дайте определение выборочного наблюдения, объясните его преимущества и необходимость.

2. Опишите способы формирования выборочной совокупности.

3. Дайте определение средней и предельной ошибок выборки.

4. Объясните разницу между повторным и бесповторным отбором.

5. Распространение выборочных данных на генеральную совокупность

Дата добавления: 2014-01-03