Территориальные индексы

Территориальные индексы – это разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям). На основе территориальных индексов выполняются международные сопоставления. Построение простейших территориальных индексов рассмотрим на примере показателя товарооборота для двух районов.

Территориальный индекс товарооборота – это отношение суммы выручки от продажи в одном из районов (А) к аналогичному показателю в другом (Б).

.

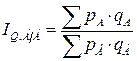Различие объемов товарооборота вызвано различием ассортимента и количества проданных товаров, а также различием цен. Территориальный индекс физического объема товарооборота рассчитывается как

.

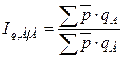Территориальный индекс цен

.

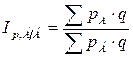В этих формулах 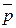– средняя межрайонная цена товара каждого вида, 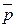= (p_А · q_А + p_Б ∙ q_Б)/(q_А + q_Б); q = (q_А+q_Б) – суммарный по двум районам объем продаж каждого вида товара. Более сложные, чем ранее, взвешивающие показатели применяются для того, чтобы результаты расчета были обратимыми, т.е. чтобы выполнялись соотношения

I_q,А/Б = 1/ I_q,Б/А и I_p,А/Б = 1/ I_p,Б/А.

Заметим, однако, что условия индексной модели

I_q,А/Б·I_p,А/Б = I_Q,А/Б

I_q,Б/А·I_p,Б/А = I_Q,Б/А

могут нарушаться, хотя, как правило, и не очень существенно.

Контрольные вопросы

1. Дайте определение индекса, назовите виды индексов

2. Задачи индексного анализа

3. Принципы построения общих индексов

4. Агрегатная форма общих индексов

5. Виды средних индексов

6. Индексы средних величин

7. Изучение структурных изменений с помощью индексного метода

8. Проблемы построения территориальных индексов

[1] Иногда, если таблица очень простая и содержание ее очевидно, название таблицы не приводится.

[2] На гистограмме (рисунок 3.8) для большей наглядности выделен начальный интервал доходов: известно, что у первых 0,3 % населения среднедушевой денежный доход не превышал 150 руб. Соответствующим образом изменилось значение плотности в интервале 150÷750 руб.

[3] Если число наблюдений в квартилях не целое, то квартильные значения признака находятся интерполяцией.

[4] Иногда обзорные рисунки включают доверительные интервалы для медианного значения, показывают средние значения и наблюдения, выделяющиеся из общей массы и т.д.

[5] Если имеются данные о площадях, и валовом сборе по каждой культуре, то определяющим будет непосредственно показатель урожайности. Преобразования выводят на логическую формулу среднего значения: отношение всего валового сбора к общей посевной площади.

[6] Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю

[7] У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со средним квадратическим отклонением s = 10 лет, “состарилась” еще на 15 лет. Теперь = 30 лет, а среднеквадратическое отклонение будет по-прежнему равно 10 лет. Совокупность, ранее бывшая неоднородной () со временем оказывается, таким образом, вполне однородной (10/30–100 = 33,3 %).

[8] Следует учитывать, что достаточно много статистических и просто экономических показателей по своему содержанию не могут изменить свое численное значение на 1. Например, доля рабочих в общей численности, доля затрат на покупные комплектующие, доля брака в производстве и т.п. В этих случаях интерпретируется изменение признака Х на 0,01 своей величины

[9] Надо иметь в виду, что при этом оценивается не сама нелинейная функция, но ее линейное преобразование, а это может вызвать смещение оценок параметров.

[10] Однокачественность уровней временного ряда предполагает, что в пределах всего изучаемого периода, к которому относятся уровни, проведена типологическая группировка. После выделения однородных групп могут использоваться и анализироваться уровни ряда.

[11] Например, численность скота в домашнем хозяйстве на 20.11.1980 г. и 20.11.1990 г. качественно различается в связи с ранней зимой 1980 г., что привело соответственно к раннему забою скота. Регистрацию таких процессов лучше выполнять в “нейтральные” даты. Это середина зимы, когда забой прекращается, и середина лета, когда процесс появления приплода стабилизируется и заканчивается.

[12] При ручных расчетах обычно уровни нумеруют таким образом, чтобы Σt = 0.

[13] Заметим, что более полные уравнения авторегрессии можно получить на основе анализа автокорреляционной функции, когда определяются число параметров (a₀, a₁, a₂,...; b₀, b₁, b₂, …) и соответствующие этим параметрам величины лагов.

[14] И наоборот, агрегатная форма общего индекса позволяет выбрать взвешивающий показатель при расчете общего индекса в виде средней величины.

Дата добавления: 2014-01-03