Простой трубопровод постоянного сечения

Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.

Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рисунок 4.1), имеет общую длину 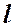и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан).

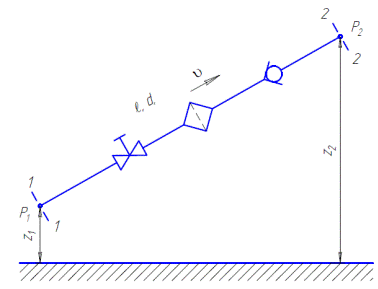
Рисунок 4.1 ─ Схема простого трубопровода

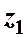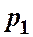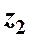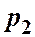В начальном сечении трубопровода 1-1 геометрическая высота равнаи избыточное давление , а в конечном сечении 2-2 ─ соответственно и . Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна .

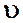Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и 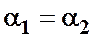, то скоростной напор можно не учитывать. При этом получим

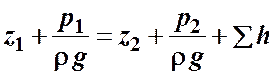
или

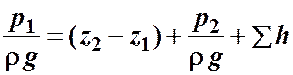. (4.1)

Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором 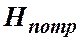. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором .

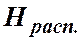Такой напор складывается из геометрической высоты 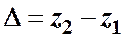, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.

Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту

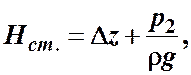
а последнее слагаемое 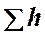─ как степенную функцию расхода

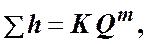
тогда

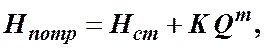(4.2)

где 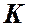─ величина, называемая сопротивлением трубопровода;

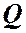─ расход жидкости;

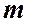─ показатель степени, который имеет разные значения в зависимости от режима течения.

Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно

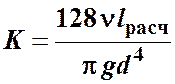и 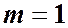, (4.3)

где .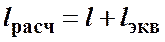

Численные значения эквивалентных длин для различных местных сопротивлений обычно находят опытным путем.

Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем

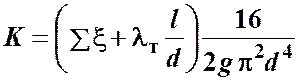и 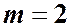. (4.4)

Формула (4.2), дополненная выражениями (4.3) и (4.4) является основной для расчета простых трубопроводов. По ней можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Н_потр.

При ламинарном течении эта кривая изображается прямой линией (рис.4.2, а), при турбулентном ─ параболой с показателем степени равном двум (рис.4.2, б).

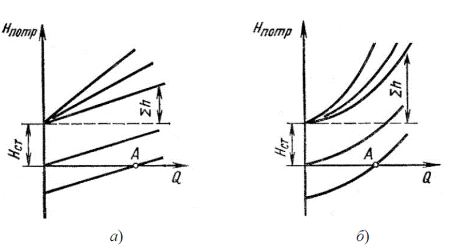
Рисунок 4.2─ Зависимости потребных напоров от расхода жидкости в трубопроводе

Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.

Величина статического напора Н_ст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.

Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.

Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:

.

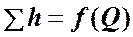Дата добавления: 2014-01-03