Уравнение состояния идеального газа

Давление газа с точки зрения МКТ.

Раскроем физический смысл и природу непосредственно наблюдаемых параметров состояния р,Т и других, исходя из молекулярно-кинетический представлений. При этом мы будем использовать статистический метод, интересуясь движением не отдельных молекул, а лишь такими средними величинами, которые характеризуют движение всей совокупности молекул.

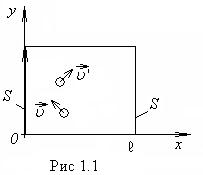Уравнение состояния идеального газа позволяет вычислять давление, объем, плотность и температуру ограниченного объема газа любого сорта. Выведем уравнение состояния идеального газа. Будем считать молекулы газа маленькими твердыми шарами, заключенными в ящик объема V. Это дает нам возможность считать, что между молекулами происходит упругое соударение. Рассмотрим сначала одну такую молекулу, отражающуюся от левой стенки ящика (рис.1.1). Средняя сила, действующая на стенку на протяжении времени 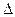t, равна 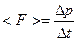. В результате удара о стенку импульс молекулы меняется на величину

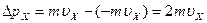- удар абсолютно упругий. Время между соударениями молекулы с этой стенкой 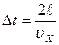, тогда .

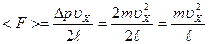В равновесном состоянии движение всех молекул хаотично. Это позволяет считать, что все молекулы движутся только в направлениях X,Y и Z, т.е. если в единице объема содержится п молекул, то в каждом из этих направлений движутся по 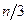молекул, или по 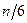в одну сторону.

Если в объеме содержится N молекул, то результирующая сила, действующая на стенку со стороны всех молекул рана 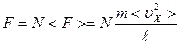, где <u_x² > - средний квадрат скорости движения всех N молекул в направлении Х.

Величина, равная корню квадратному из <u_X² > называется среднеквадратичной скоростью молекулы в направлении Х.

Разделив обе части этого уравнения на площадь стенки S, получим выражение для давления:

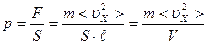, где V – объём газа (ящика).

Мы получили, что для данной массы газа произведение pV остается постоянным при условии, что кинетическая энергия частиц остается без изменения (сохраняется). Это закон Бойля.

Молекулы газа движутся хаотически во всех направлениях, поэтому все направления в пространстве равноправны, и

.

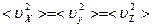Ясно, что 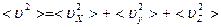, поэтому ,

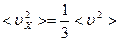тогда

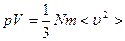. (1.1)

Это основное уравнение молекулярно - кинетической теории.

Абсолютной температурой принято называть величину, прямо пропорциональную средней кинетической энергии молекул в сосуде:

,

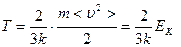где k - постоянная Больцмана, k =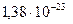Дж/К, E_K - средняя кинетическая энергия, приходящаяся на одну частицу.

Тогда уравнение (1.1) можно записать в виде

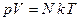, (1.2)

Или .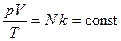

Таким образом, применив уравнения классической механики к молекулам идеального газа, мы вывели уравнение его состояния.

Согласно закону Авогадро, моли всех газов занимают при одинаковых условиях одинаковый объем, поэтому для моля вещества константа в уравнении будет одинакова для всех газов:

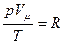, (1.3)

индекс m означает, что данный параметр берется в расчете на моль вещества, R - универсальная газовая постоянная, R =8,31 Дж/(моль∙К)

Для произвольной массы газа m уравнение состояния идеального газа примет вид:

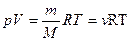
- уравнение Менделеева – Клапейрона, где μ – молярная масса, ν - число молей (количество вещества).

Отношение 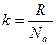- это постоянная Больцмана. Здесь 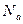– число Авогадро. Умножим правую часть уравнения (1.3) на 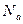. Произведение 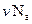равно числу молекул в массе газа m, тогда

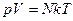, (1.4)

разделив на V c учетом того, что N/V - число молекул в единице объема, получаем

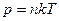. (1.5)

Выражения (1.1), (1.2), (1.4), (1.5) – это уравнения состояния идеального газа.

Дата добавления: 2014-01-03