В случае парной зависимости

Зная показатели тесноты корреляционной связи, можно решать следующие группы вопросов:

1. о необходимости изучения данной связи между признаками и целесообразности ее практического применения;

2. сопоставляя показатели тесноты связи для различных ситуаций, можно судить о степени различий в ее проявлении для конкретных условий;

3. сопоставляя показатели тесноты связи результативного признака с различными факторами, можно выявить те факторы, которые в данных условиях являются решающими и главным образом воздействуют на формирование величины результативного признака.

К простейшим показателям тесноты связи относят коэффициент корреляции знаков, который был предложен немецким ученым Г. Фехнером (1801-1887). Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Коэффициент Фехнера можно записать следующим образом:

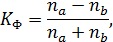
где - число совпадений знаков отклонений индивидуальных значений от средней; 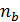- число несовпадений знаков отклонений индивидуальных значений от средней.

Коэффициент Фехнера может принимать значения в пределах от -1 до +1. Если знаки всех отклонений совпадут, то 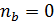и тогда 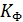=1, что свидетельствует о возможном наличии прямой связи. Если же знаки всех отклонений будут разными, то тогда 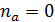и 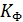=-1, что дает основание предположить наличие обратной связи.

Для нашего примера

№ фирмы	Затраты на рекламу (х)	Количество туристов (y)	Знаки отклонений признака от средней	Совпадение (а) или несовпадение (в) знаков
для х	для y
			-	-	а
			-	-	а
			-	-	а
			-	-	а
			-	-	а
			-	-	а
			-	-	а
			-	-	а
			+	-	в
			+	+	а
			+	-	в
			+	+	а
			+	-	в
			+	-	в
			+	+	а
			+	+	а
			+	+	а
			+	+	а
			+	+	а
			+	+	а
среднее	9,95	992,5

В данном случае 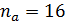, а 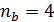. Рассчитаем коэффициент Фехнера:

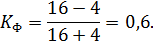
Полученная величина коэффициента Фехнера свидетельствует о том, что можно предполагать наличие прямой зависимости между исследуемыми признаками.

Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции:

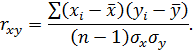
Или после преобразований

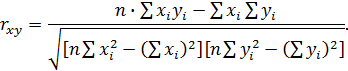
Линейный коэффициент корреляции характеризует тесноту связи между признаками и может принимать значения от +1 до -1. Чем ближе коэффициент корреляции по модулю к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи: прямой зависимости соответствует знак плюс, а обратной – знак минус.

Существует следующая шкала:

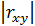
	<0,15	0,16-0,20	0,21-0,30	0,31-0,40	0,41-0,50	0,51-0,80	0,81-0,90	0,91-1,00
связь	отсутст-вует	плохая	слабая	умеренная	средняя	высокая	очень высокая	полная

Для нашего примера 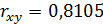, что говорит о возможном наличии достаточно тесной прямой зависимости между затратами на рекламу и количеством туристов, воспользовавшихся услугами фирмы.

Квадрат коэффициента корреляции называется коэффициентом детерминации. Для нашего примера 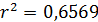, что означает что 65,69% вариации числа клиентов, объясняется вариацией затрат фирм на рекламу своих услуг.

Для того, чтобы можно было распространить выводы, полученные по результатам выборки, на всю генеральную совокупность, необходимо оценить значимость (существенность) линейного коэффициента корреляции.

Для определения значимости линейного коэффициента корреляции можно использовать t-критерий Стьюдента:

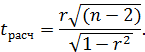
Полученное значение t-критерия Стьюдента сравнивают с табличным значением t-критерия (число степеней свободы равно ).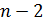

Если 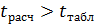, то практически невероятно, что найденное значение обусловлено лишь случайными совпадениями х и y в выборке из генеральной совокупности, для которой действительное значение коэффициента корреляции равно нулю. Таким образом, если 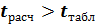, то полагают, что линейный коэффициент корреляции значим и его можно распространить на генеральную совокупность.

Если же 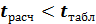, то считают, что линейный коэффициент корреляции не значим и в генеральной совокупности он существенно не отличается от нуля.

Для нашего примера

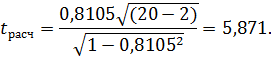
Табличное значение для числа степеней свободы 18 и уровня значимости 0,01 (1%) равно 2,878. Таким образом, лишь с вероятностью менее 1% можно утверждать, что величина 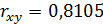могла появиться в силу случайности выборки. Т.е. с вероятностью 99% можно считать, что в генеральной совокупности действительно существует тесная прямая зависимость между изучаемыми признаками.

Дата добавления: 2014-01-03