Диффузия в газах. Закон Фика

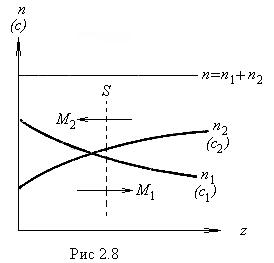
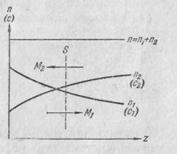
Предположим, что в единице объема двухкомпонентной газовой смеси содержится п ₁ молекул одного вида и п ₂ молекул другого вида. Полное число молекул в единице объема равно п = п ₁ + п ₂. Отно­шение 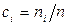называется относительной концентрацией моле­кул i -го вида. Допустим, что в направлении оси z создаются градиенты кон­центраций dc ₁ /dz и dc₂/dz, причем dc ₁ /dz = — dc₂/dz (рис.2.8.). Тогда

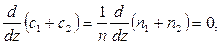
так что п, а следовательно, и р постоянны (р = nkT). В этом случае газодинамических потоков не возникает. Однако вследствие теплового движения молекул будет происходить процесс вы­равнивания концентраций, сопровож­дающийся переносом массы каждой из компонент в направлении убывания ее концентрации. Этот процесс носит наз­вание диффузии. Диффузия наблю­дается также в жидких и твердых телах. Поток молекул i -го вида через перпен­дикулярную к оси z поверхность S оп­ределяется выражением

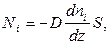(2.9)

где D — коэффициент пропорциональности, называемый коэф­фициентом диффузии. Знак минус указывает, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i -го вида m_i, получим выражение для потока массы i -й компоненты:

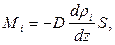(2.10)

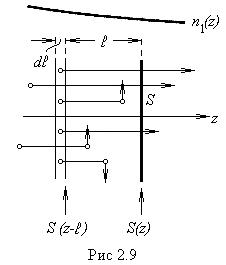где ρ_i = n_im_i — парциальная плотность i -й компо­ненты; ее называют также абсолютной концентра­цией.

Формулы (2.9) и (2.10) представляют собой эмпирические урав­нения диффузии. Их называют также законом Фика.

Получим уравнение диффузии, основываясь на молекулярно-кинетических представлениях, причем для упрощения расчетов будем считать, что молекулы обеих компонент мало отли­чаются по массе (m ₁ 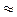m ₂ 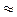m) и имеют практически одинаковые эффективные сечения (σ₁ 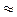σ₂ 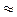σ). В этом случае молекулам обеих компонент можно приписывать одинаковую среднюю скорость теп­лового движения 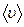, а среднюю длину свободного пробега вычис­лять по формуле 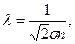где n = n ₁ + n ₂. Пусть изменение концентрации первой компоненты вдоль оси z задано функцией n ₁ = n ₁ (z) (рис.2.9). Через поверхность S будут пролетать в положительном направ­лении оси z молекулы, претерпевшие последнее соударение на раз­личных расстояниях 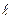от S. Разобьем все пространство слева от S на слои толщины d 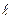(рис. 2.9). Полный по­ток молекул через поверхность S можно получить, просуммировав по­токи, создаваемые молекулами, испы­тавшими последнее соударение в та­ких слоях.

Из слоя толщины d 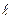начинают свой полет к поверхности S те мо­лекулы первой компоненты, которые претерпевают в этом слое столкнове­ние с другими молекулами. Их чис­ло равно

Рис 132.1

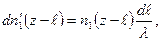
где z — координата плоскости S (d 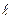/ λ есть вероят­ность претерпеть соударение на пути d 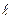). Эти молекулы создают через поверхность S (z – 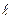)) поток

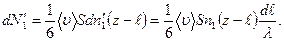
Из числа молекул, летящих в этом потоке, достигает поверх­ности S без столкновений и, следовательно, проникает в пространство, расположенное справа от S, количество молекул, равное

.

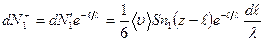(е ^{– l /λ} есть вероятность того, что молекула пролетает путь 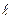без столкновений). Знак «+» при dN ₁ указывает на то, что имеются в виду молекулы, летящие в положительном направлении оси z.

Полный поток молекул первой компоненты через поверхность S получим, проинтегрировав это выражение по :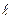

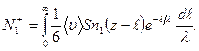
Воспользовавшись быстрым спадом экспоненты и малостью λ, пред­ставим стоящую под знаком интеграла функцию n ₁(z – 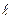) в виде

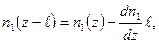
где dn ₁/ dz — производная в точке с координатой z. Тогда

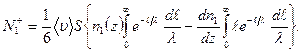
Первый интеграл есть единица, второй равен λ. Следовательно,

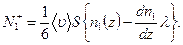
Поток молекул первой ком­поненты, летящих через поверхность S в отрицательном направле­нии оси z,

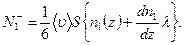
Результирующий поток молекул первой компоненты через по­верхность S в направлении оси z равен разности этих потоков

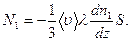(2.11)

Мы получили уравнение (2.9), причем коэффициент диффузии

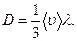(2.12)

При этом коэффициент диффузии для обеих компонент имеет одинаковое значение.

Подставив в (2.11) выражения для 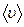и λ, можно получить, что

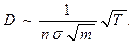
В отличие от η и κ коэффициент диффузии оказывается обратно пропорциональным числу молекул в единице объема, а следовательно, и давлению р:

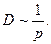
Зависимость от температуры у D такая же, как у η и κ.

Так как мы полагали молекулы обеих компонент одинаковыми по массе к эффективному сечению, (2.12) представляет собой, по суще­ству, выражение для коэффициента самодиффузии, т. е. диффузии молекул некоторого газа в среде молекул того же газа. Явление са­модиффузии можно было бы наблюдать, пометив каким-то способом часть молекул однородного газа. Тогда в случае, если бы концентра­ция меченых молекул и молекул, не несущих отметки, была непо­стоянна, в газе возникли бы встречные потоки разного рода моле­кул, причем величина потоков определилась бы формулой (2.11). Для смеси молекул различной массы и сечения соответствующий расчет дает следующее выражение коэффициента диффузии:

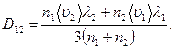
Здесь n ₁, 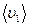, λ₁ — концентрация, средняя скорость и средняя длина свободного пробега молекул первого вида, n ₂, 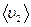, λ₂ — те же величины для молекул второго вида.

Дата добавления: 2014-01-03