Основные теоремы о пределах

Лекция № 3

Тема: «Основные теоремы о пределах»

1. Основные теоремы о пределах 2. Предел промежуточной величины 3. Второй замечательный предел. Числовая последовательность и ее предел. 4. Третий, четвертый и пятый замечательные пределы 5. Виды неопределенностей и их раскрытие  

Т.1.1. Предел алгебраической суммы конечного числа функций, имеющих предел в точке 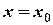равен алгебраической сумме пределов этих функций в этой точке, т.е.

.

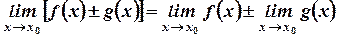Т.1.2. Предел произведения конечного числа функций, имеющих предел в точке 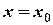равен произведению пределов этих функций в рассматриваемой точке

.

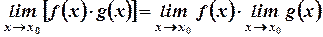Т.1.3. Предел постоянной величины равен самой постоянной

.

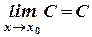Следствие 1: постоянный множитель можно выносить за знак предела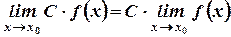

Следствие 2: предел целой положительной степени функции равен той же степени предела этой функции

.

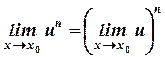Т.1.4. Предел частного двух функций, имеющих предел в точке 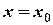равен частному от деления пределов этих функций при условии, что предел знаменателя отличен от нуля, т.е.

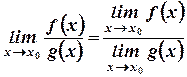, причем .

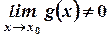Доказательство

Дано: , .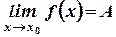

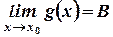Доказать: .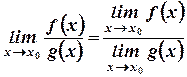

По второму определению предела можем записать

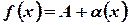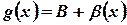, , где 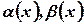- бесконечно малые величины. Рассмотрим разность

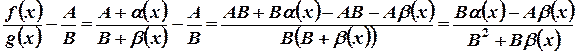. (1) Дробь 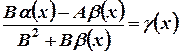- бесконечно малая, т.к. числитель есть алгебраическая сумма бесконечно малых величин, а знаменатель имеет предел равный .

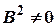Следовательно .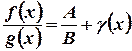

В силу второго определения предела и теоремы об эквивалентных бесконечно малых .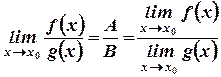

Рассмотрим теоремы, облегчающие вычисление пределов.

Дата добавления: 2014-01-03