Алгебра логики

Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними [1].

Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, «6 – четное число» - высказывание, т.к. оно истинно, а предложение «Рим – столица Франции» тоже высказывание, т.к. оно ложное.

Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания и называются логическими связками.

Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:

Операция «НЕ» называется отрицанием и обозначается чертой над высказыванием ( или знаком ¬). Высказывание 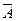истинно, когда 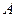ложно, и ложно, когда 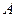истинно. Например, «Луна спутник Земли» (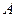); «Луна не спутник Земли» ().

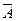Операция «И» называется конъюнкцией или логическим умножением и обозначается * ( или знаком 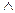или&). Высказывание 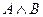истинно тогда и только тогда, когда оба высказывания 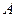и 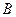истинны. Например, «(10 делится на 2) и (5 больше 3)» истинно, а высказывания «(10 делится на 2) и (5 не больше 3)», «(10 не делится на 2) и (5 больше 3)», «(10 не делится на 2) и (5 не больше 3)» ложны.

Операция «ИЛИ» называется дизъюнкцией или логическим сложением и обозначается + ( или знаком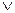). Высказывание 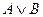ложно тогда и только тогда, когда оба высказывания 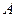и 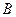ложны. Например, высказывание «(10 не делится на 2) или (5 не больше 3)» ложно, а высказывания «(10 делится на 2) или (5 больше 3)», «(10 делится на 2) или (5 не больше 3)», «(10 не делится на 2) или (5 больше 3)» истинны.

Операция, выражаемая связками «если …, то», «из … следует», «… влечет …», называется импликацией и обозначается знаком 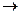. Высказывание 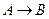ложно тогда и только тогда, когда 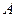истинно, а 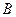ложно.

Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «… равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком 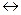или ~. Высказывание 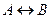истинно тогда и только тогда, когда значения 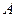и 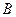совпадают.

Высказывания 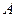и 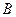, образующие составное высказывание 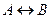, могут быть совершенно не связаны по содержанию.

Импликацию можно выразитьчерез дизъюнкцию и отрицание:

.

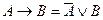Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:

.

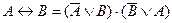Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.

2. Логическая формула

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить логической формулой. Определение логической формулы:

· Всякая логическая переменная и символы «истина» («1») и «ложь» («0») – формулы.

· Есл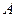и и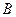формулы, то 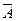, (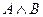), (), (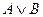), ()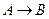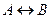– формулы.

· Никаких других формул в алгебре логики нет.

3. Связь между алгеброй логики и двоичным кодированием

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: «1» и «0». Отсюда следует два вывода:

· Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных.

· На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.

Дата добавления: 2014-01-03