Интеграл Клаузиуса

Интегральным уравнением второго начала термодинамики для равновесных круговых процессов является интеграл Клаузиуса.

Для термического КПД обратимого цикла Карно можно записать:

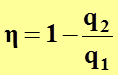(4.16)

или

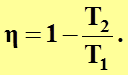(4.17)

Таким образом,

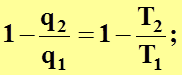(4.18)

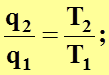(4.19)

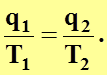(4.20)

Отметим, что 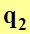─ величина отрицательная, поэтому с учетом знака можно записать, что

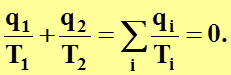(4.21)

Величина 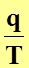называется приведенной теплотой.

Таким образом, в обратимом цикле Карно сумма приведенных теплот равна нулю.

Можно доказать, что полученное равенство верно не только для цикла Карно, но и для любого обратимого цикла. При этом рассматриваемый произвольный обратимый цикл разбивается на большое количество элементарных циклов Карно, для каждого из которых верно равенство:

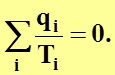(4.22)

Если произвести разбиение на бесконечно большое количество элементарных циклов, то в пределе получим, что

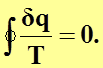(4.23)

Выражение (4.23) представляет собой интеграл Клаузиуса для обратимых круговых процессов.

Для необратимых циклов термический КПД можно вычислить только по формуле (4.16).

Из неравенства 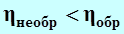следует, что

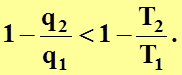(4.24)

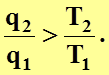(4.25)

Следовательно,

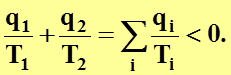(4.26)

Для произвольного необратимого цикла по аналогии можно получить, что

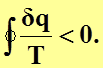(4.27)

Выражение (4.27) представляет собой интеграл Клаузиуса для необратимых процессов.

Объединяя оба интеграла можно записать, что

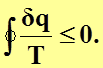(4.28)

Подынтегральное выражение при этом представляет собой полный дифференциал некоторой функции (энтропии).

Таким образом, для обратимых процессов

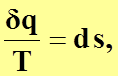(4.29)

а для необратимых процессов

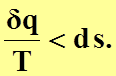(4.30)

Обобщая выражения (4.29) и (4.30) получаем, что

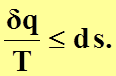(4.31)

Следовательно, для замкнутой системы, для которой :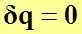

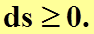(4.32)

Таким образом, энтропия замкнутой системы в необратимых процессах остается неизменной, а в обратимых процессах увеличивается.

Дата добавления: 2014-01-03