Дифференцирование функций одной переменной

Лекция 5. Начала дифференциального исчисления.

Во многих прикладных задачах важную роль играет изучение поведения функций «в малом», т.е. в достаточно малых окрестностях каждой точки области определения. Исследование функций «в малом» составляет предмет раздела математического анализа, называемого дифференциальным исчислением.

Основной принцип дифференцирования достаточно прост. Представим себе, что функция y = f(x) такова, что ее графиком является непрерывная кривая без изломов типа разрывов 1-го рода. Если взять достаточно малый интервал оси х, примыкающий к точке х₀ на котором кривая y = f(x) не очень сильно изгибается, то можно считать, что отрезок графика близок к отрезку прямой. Чем меньше интервал на оси х, тем ближе «кусочек» графика к прямолинейному. Следовательно, любая «гладкая» функция, сколь угодно нелинейная, всегда может рассматриваться на достаточно малом интервале значений аргумента как линейная. Это и есть основной принцип дифференциального исчисления.

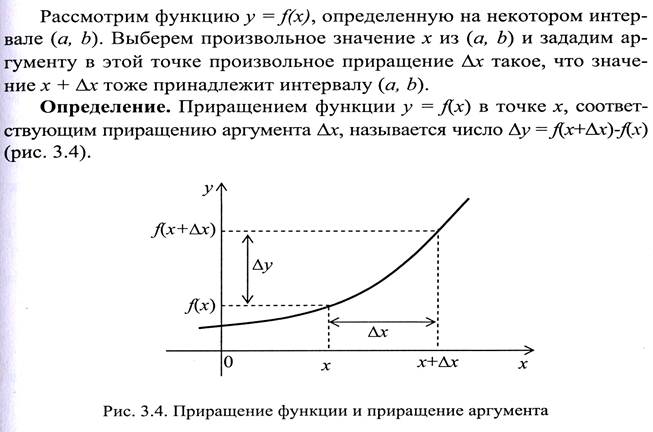
Придадим приведенным рассуждениям более строгую форму.

Введя приращения аргумента и функции, можно теперь дать определение производной — ключевого понятия дифференциального исчисления.

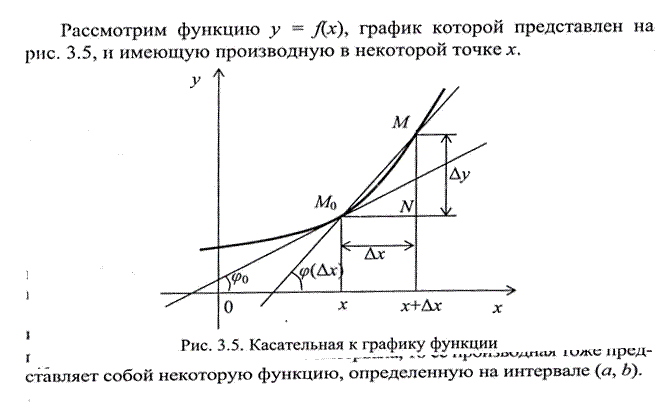
Введенному понятию производной легко придать геометрический и физический смысл.

Пользуясь понятием производной, можно строго определить касательную к кривой (а ведь как трудно было дать строгое определение касательной в геометрии!).

Теперь рассмотрим физический смысл производной.

Если функция f(x) имеет смысл заряда, протекающего через поперечное сечение проводника за время х, то производная 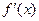имеет смысл мгновенного значения силы тока, протекающего в момент времени х через поперечное сечение проводника.

Поскольку производная определяется как предел отношения приращений, можно ввести понятие левой и правой производных.

Определим теперь понятие дифференцируемости функции.

Опираясь на это определение, нетрудно доказать следующую теорему.

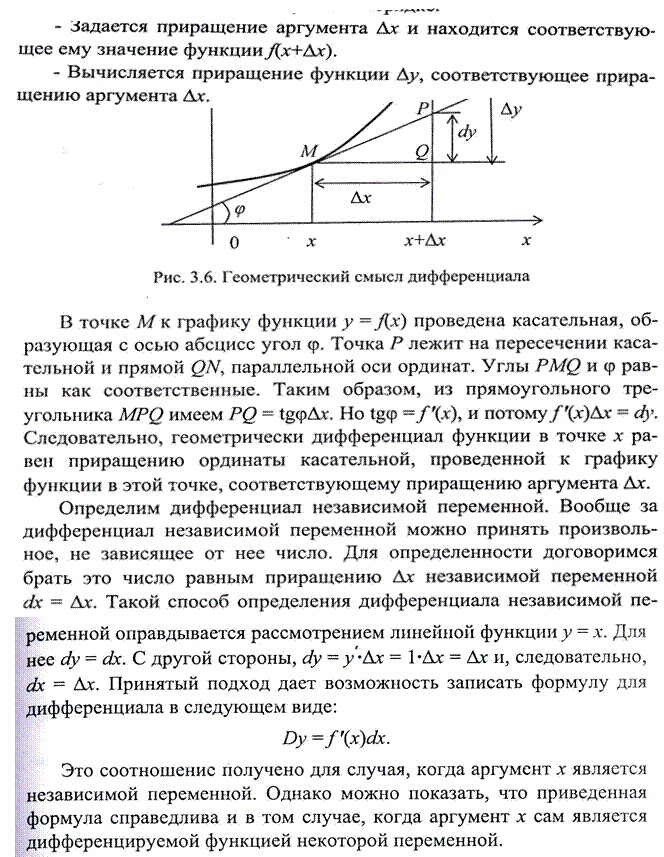
Нахождение производных, если это не оговаривается особо, основывается на определении производной. Именно,

Вычисление производных «по определению» может оказаться излишне трудоемкой процедурой, поэтому были разработаны описанные ниже правила дифференцирования, зачастую существенно упрощающие задачу.

5. Производная обратной функции.

Весьма эффективными приемами при вычислении производных являются способы вычисления производных сложной функции, функции, заданной параметрически и функции неявной.

Теперь вспомним, как мы записывали уравнение прямой, и найдем уравнения касательной и нормали к графику функции в данной точке.

Обратим внимание на то, что производная от функции сама является функцией, от которой можно брать производную. Операция может быть повторена много раз, отсюда следует вычисление производных высших порядков.

Важнейшим применением дифференцирования является разложение функций в ряд Тейлора.

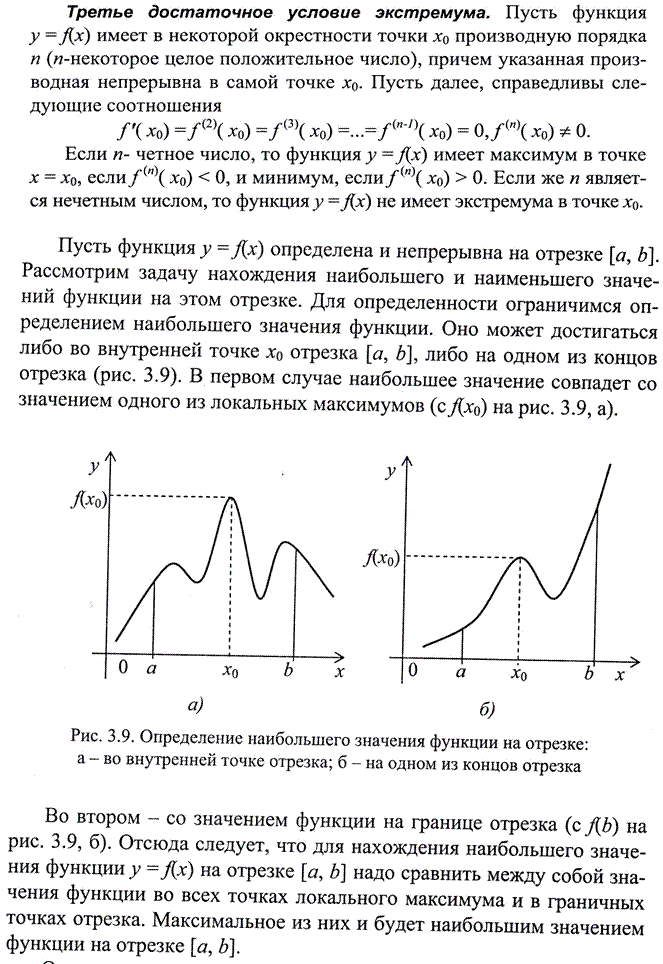
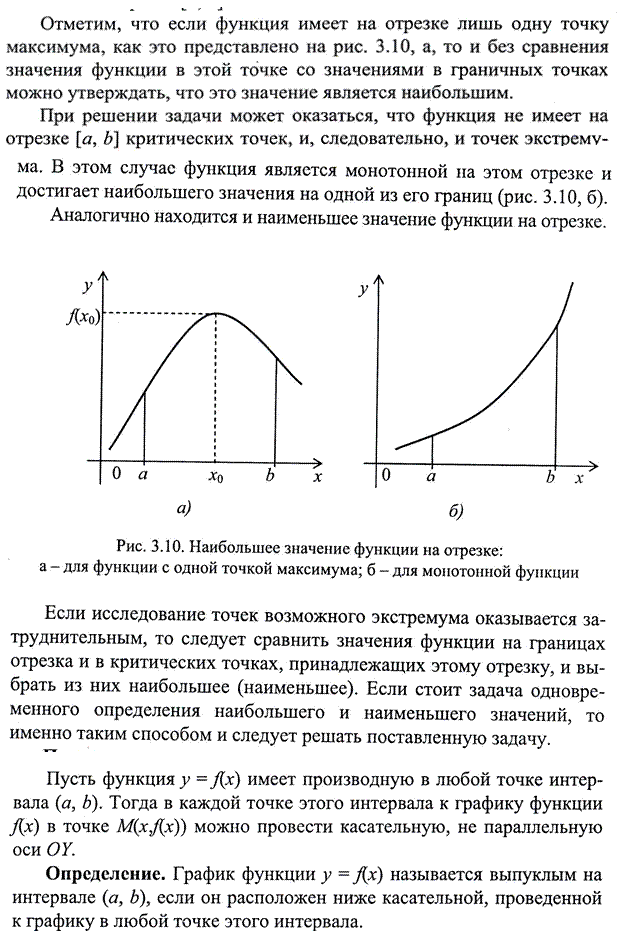
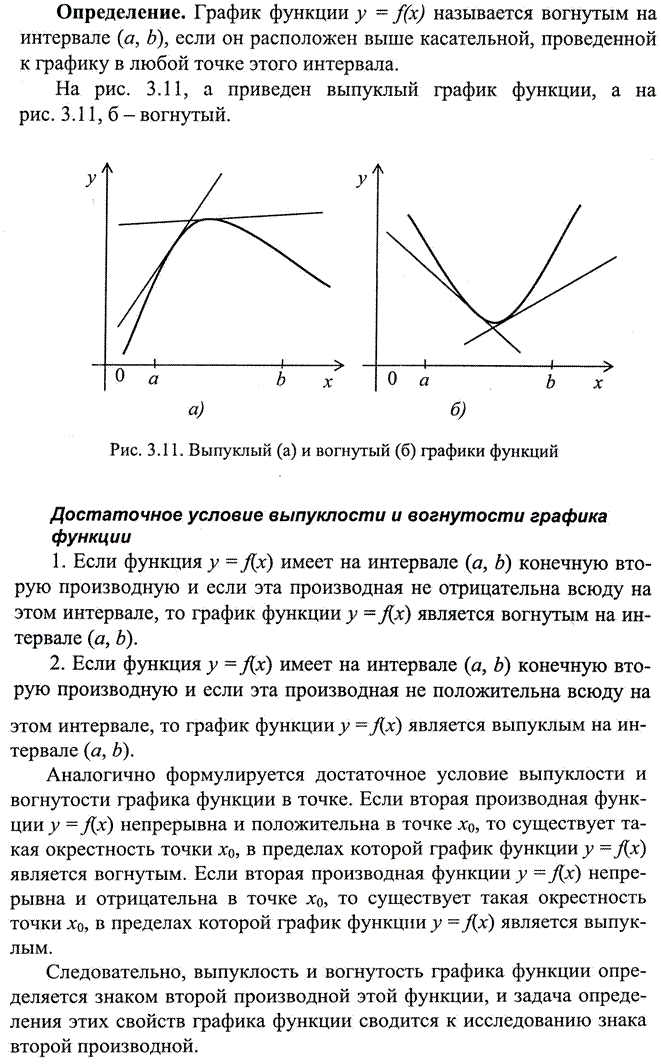
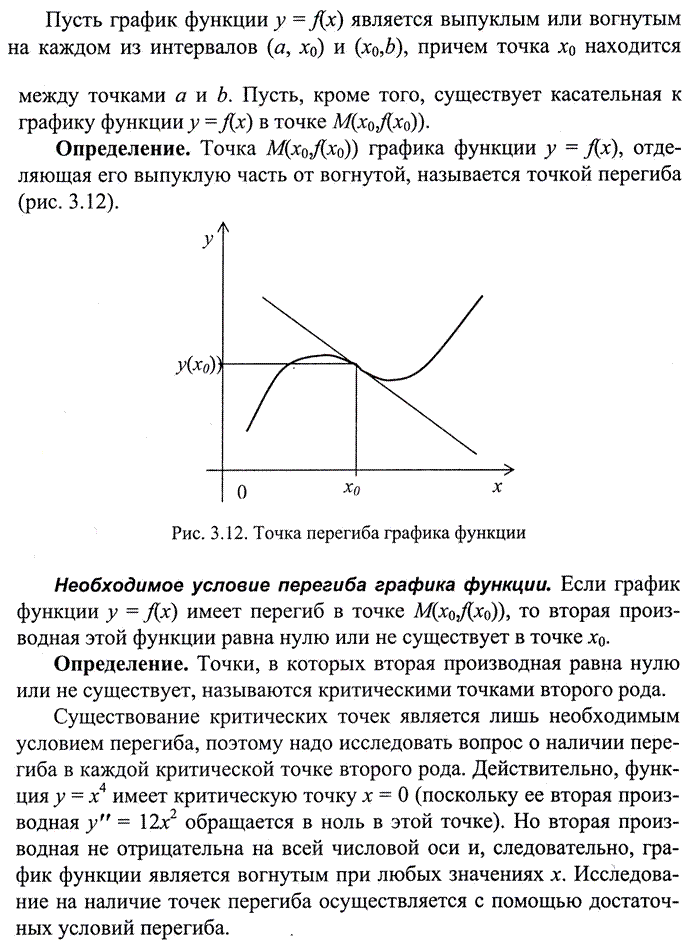
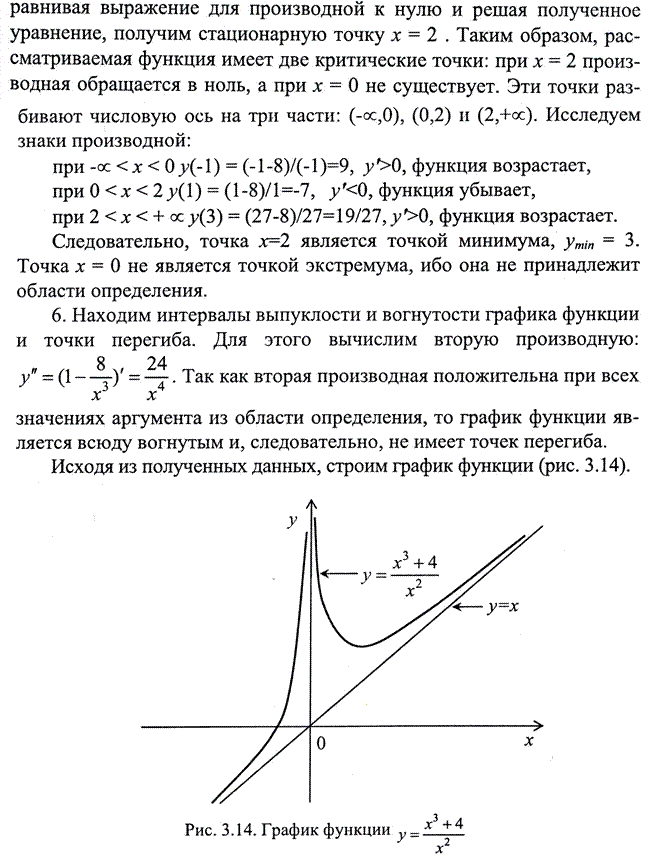
Дифференцирование позволяет резко расширить возможности исследования функций и построения графиков.

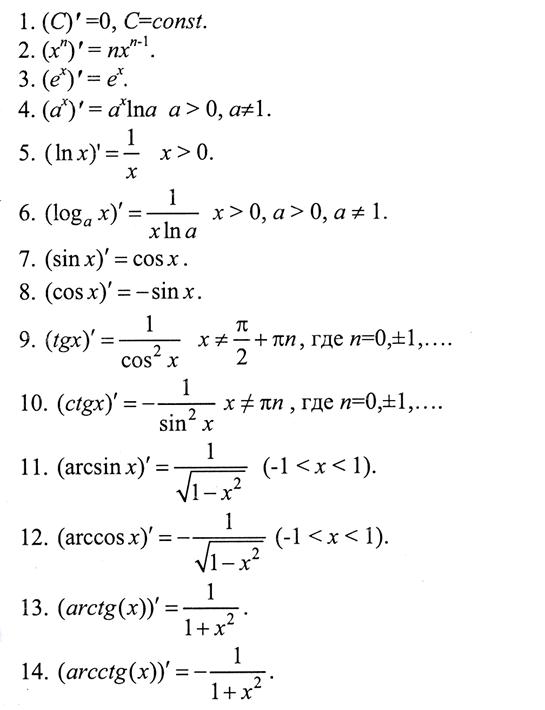В заключение приведем таблицу производных некоторых основных функций

Дата добавления: 2014-01-03