Необходимое условие дифференцируемости

Рассмотрим теорему, связывающую операцию дифференцирования с непрерывностью функции.

0.4.1. Если функция дифференцируема в точке 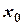, то в этой точке она непрерывна.

Доказательство:

Дано: .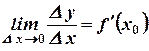

Доказать: функция 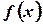- непрерывна в точке .

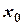Т.к. существует 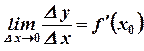, то по второму определению предела

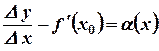- бесконечно малая при .

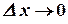Отсюда 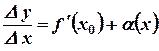или .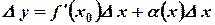

Найдем .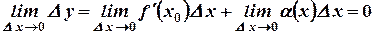

Так как бесконечно малому приращению аргумента 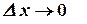соответствует бесконечно малое приращение функции, то по определению непрерывной функции следует непрерывность функции 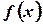в точке .

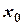Обратная теорема не верна!

Существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми.

Пример 1. Рассмотрим функцию 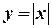. В точке 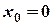она непрерывна т.к.

1) ;

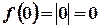2)

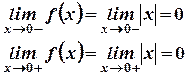
3)

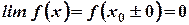
Покажем, что функция 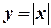не имеет производной в точке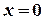

1) ;

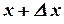2)

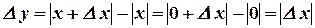
3)

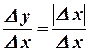
4)

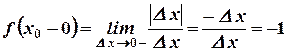
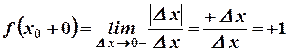
Следовательно, предел отношения 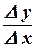не существует, т.к. 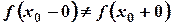, тогда не существует и производная функции в точке .

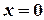Пример 2. Функция 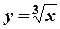непрерывна в любой точке числовой оси.

1) Пусть , .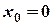

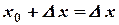2)

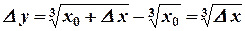
3)

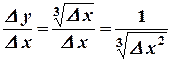
4) 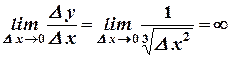- не существует.

Дата добавления: 2014-01-03