
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Мгновенный центр скоростей
|
|
|
|
Теорема (следствие)2. Концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.
Исходя из теоремы о скоростях точек при плоском движении тела, имеем
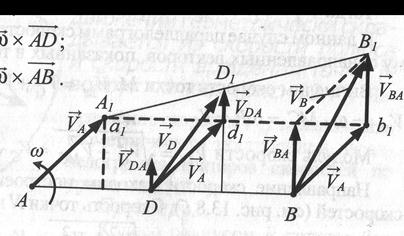
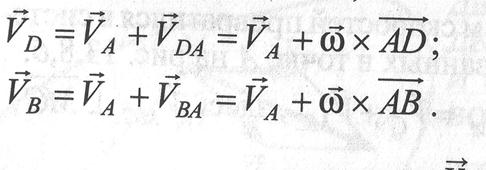
Тогда 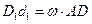 и
и 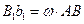 и, следовательно,
и, следовательно,
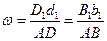 или
или 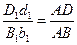 .
.
Т.к. 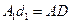 и
и 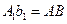 как противоположные стороны параллелограммов, то
как противоположные стороны параллелограммов, то 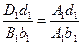 . Это соотношение показывает, что
. Это соотношение показывает, что 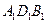 - отрезок прямой. Из подобия
- отрезок прямой. Из подобия 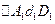 и
и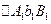 имеем
имеем
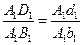 или
или 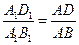 и
и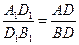 ,
,
т.е. расстояния между концами векторов скоростей пропорциональны расстояниям между соответствующими точками.
Задача 1. Для механизма, изображенного на рис., найти скорость точки В, если скорость точки А равна 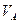 , угол
, угол 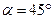 .
.
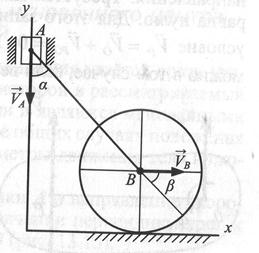
Решение. При движении ползуна А в направлении 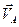 колесо катится вправо и точка В имеет скорость
колесо катится вправо и точка В имеет скорость 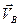 . Углы
. Углы 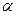 и
и 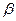 образованы векторами
образованы векторами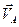 и
и 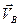 с прямой АВ. При
с прямой АВ. При 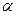 =
=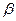 =45°
=45° 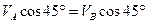 , откуда
, откуда 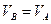 .
.
Задача 2. Кривошип ОА (рис. 13.12) длиной 1 м вращается с угловой скоростью 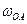 = 2рад/с. Определить скорость точки В.
= 2рад/с. Определить скорость точки В.
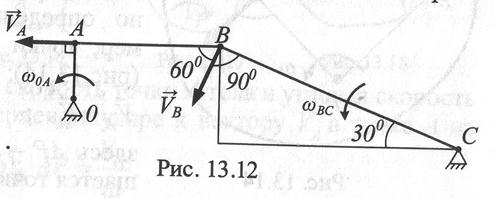
Решение. При заданном направлении вращения кривошипа ОА его скорость будет определяться вектором 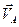 . Величина скорости
. Величина скорости 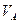 =
=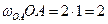 м/с.
м/с.
Кривошип ВС при этом будет вращаться вокруг точки С угловой скоростью 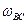 , и скорость точки В определится вектором
, и скорость точки В определится вектором 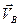 .
.
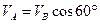 , откуда
, откуда 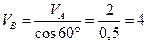 м/с.
м/с.
Теорема. В каждый момент времени при плоском движении тела, если 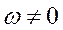 , имеется единственная точка в плоскости его движения, скорость которой равна нулю.
, имеется единственная точка в плоскости его движения, скорость которой равна нулю.
Эту точку называют мгновенным центром скоростей (МЦС). Обозначим её Р. Для доказательства теоремы обратимся к теореме о сложении скоростей. На рис. точка О имеет скорость 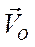 , а тело - угловую скорость
, а тело - угловую скорость 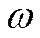 заданного направления. Требуется найти такую точку Р, скорость которой равна нулю. Для этого запишем теорему, удовлетворяя заданное условие
заданного направления. Требуется найти такую точку Р, скорость которой равна нулю. Для этого запишем теорему, удовлетворяя заданное условие 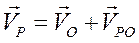 = 0. Равенство нулю этого выражения возможно в том случае, если векторы
= 0. Равенство нулю этого выражения возможно в том случае, если векторы 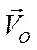 и
и 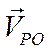 будут в точке Р равны по модулю и противоположны друг другу по направлению:
будут в точке Р равны по модулю и противоположны друг другу по направлению: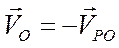 . Если
. Если 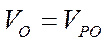 ;
; 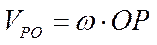 , то
, то 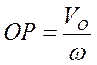 .
.
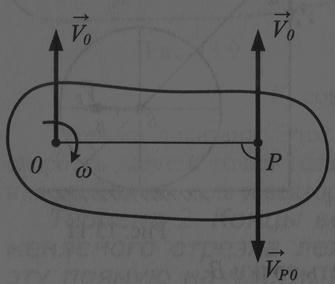
Таким образом, точка Р – МЦС на рис. находится на перпендикуляре к вектору 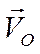 справа на расстоянии ОР. Именно в этой точке векторы
справа на расстоянии ОР. Именно в этой точке векторы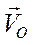 и
и 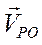 равны друг другу по модулю и противоположны по направлению, поэтому скорость точки Р равна нулю.
равны друг другу по модулю и противоположны по направлению, поэтому скорость точки Р равна нулю.
Если положение МЦС известно, то, приняв его за полюс Р, можно определить скорость, например, точки А следующим образом:
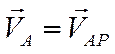 ;
; 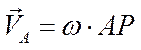 ;
; 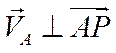 ,
,
здесь AP – радиус, на котором вращается точка А относительно МЦС.
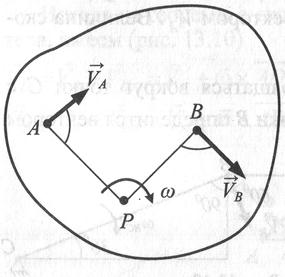
Скорость точки В вычислим аналогично:
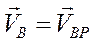 ;
; 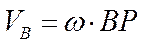 ;
; 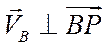 .
.
Из полученных выражений для 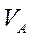 и
и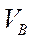 имеем
имеем
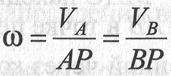 или
или 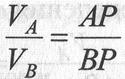 .
.
Следовательно, если положение МЦС известно, то скорости точек тела вычисляют так же, как и в случае вращения тела в плоскости вокруг МЦС с угловой скоростью 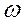 . При этом скорости точек тела пропорциональны расстояниям от точек до МЦС. Таким образом, задача расчёта скоростей точек плоской фигуры упрощается, если известно положение мгновенного центра скоростей тела в любой момент времени.
. При этом скорости точек тела пропорциональны расстояниям от точек до МЦС. Таким образом, задача расчёта скоростей точек плоской фигуры упрощается, если известно положение мгновенного центра скоростей тела в любой момент времени.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 654; Нарушение авторских прав?; Мы поможем в написании вашей работы!