Находим

,

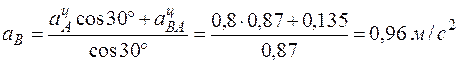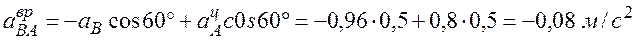
Минус показывает, что вектор 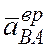направлен в сторону, про­тивоположную направлению, выбранному на рис. 17.

Определим угловое ускорение шатуна АВ:

.

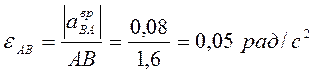Направление 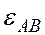будет по часовой стрелке. Определим ус­корение точки С, выбрав за полюс точку А. Вектор 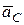разложим по выбранным осям координат:

.

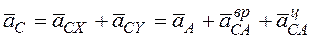Находим 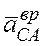и :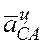

,

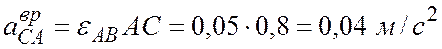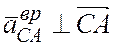и направлен в соответствии с .

,

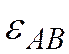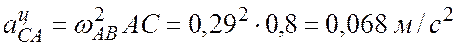вектор 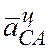направлен по СА от точки С к полюсу А.

Проецируем выражение (11) на оси координат:

,

,

.

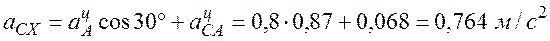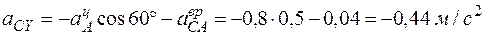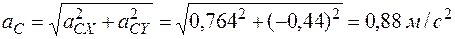Мгновенный центр ускорений (МЦУ) — это точка в плоско­сти движения плоской фигуры, ускорение которой равно ну­лю.

Для построения МЦУ при известных ускорении точки пло­ской фигуры, угловых скорости и ускорении необходимо (рис. 19):

1. Определить угол 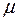по формуле: .

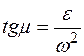2. Повернуть вектор ускорения точки на угол 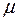, в направле­нии углового ускорения.

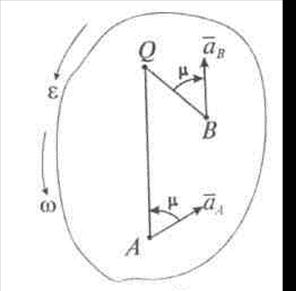
Рис. 19

3. Отложить отрезок AQ:

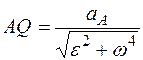
по направлению повернутого вектора ускорения 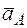. С помощью МЦУ можно найти ускоре­ние любой точки. Для этого находим вели­чину ускорения точки В:

.

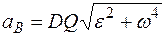От отрезка BQ под углом 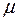откладываем в направлении, противоположном угловому ускорению, вектор ускорения точки В (рис. 19). МЦУ и МЦС в общем случае — раз­ные точки.

Задача 7. Колесо радиуса R = 0,5 м катится без скольжения равнозамедленно по прямолинейному горизонтальному рельсу. Скорость центра колеса 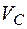= 0,5 м/с. Ускорение центра 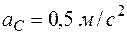. Найти ускорение точки А с помощью МЦУ и по теореме об ус­корениях точек плоской фигуры.

Решение. Находим угловые скорость и ускорение колеса:

,

.

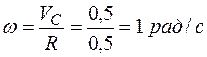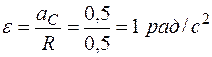Угловая скорость направлена по часовой стрелке, так как вектор скорости 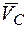относительно МЦС поворачивается по часо­вой стрелке. Угловое ускорение направлено противоположно в со­ответствии с направлением вектора ускорения центра колеса .

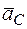I способ. Определим угол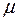

.

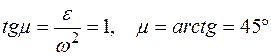Повернем 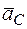на угол 45° по направ­лению углового ускорения. Определим расстояние от точки С до МЦУ (рис. 20):

.

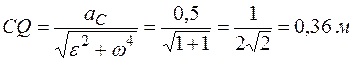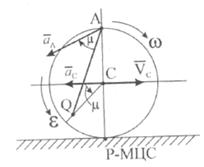
Рис. 20

Находим расстояние точки А до МЦУ из :

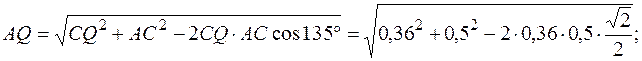
AQ =0,8 м.

В точке А от отрезка AQ отложим вектор ускорения точки А в направлении, противоположном угловому ускорению. Величи­на ускорения точки А равна:

.

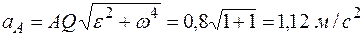II способ. Применим формулу (6), приняв за полюс точку С:

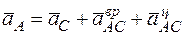. (12)

Находим , :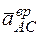

,

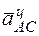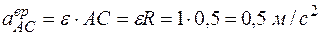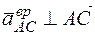и направлен в соответствии с угловым ускорением (рис. 21):

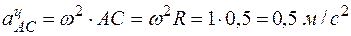
Вектор 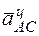направлен от точки А к полюсу С (рис. 21).

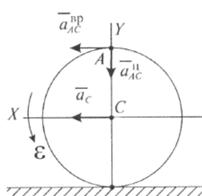
Рис.21

Проектируем выражение (12) на выбранные оси координат:

,

,

.

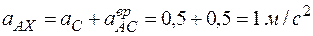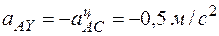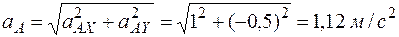Дата добавления: 2014-01-03