Точка на поверхности многогранника

При построении проекций точек на поверхности (ребре или грани) многогранника необходимо следовать аксиомам принадлежности (принадлежность точке прямой и принадлежность точки плоскости). Проекции точек должны принадлежать соответствующим проекциям ребер. На рис.3 построены проекции точки D, принадлежащей профильному ребру SB боковой поверхности пирамиды. Проекция точки D₂ задана, для построения проекции D₁ используется вспомогательная прямая, которая параллельна ребру основания ВС.

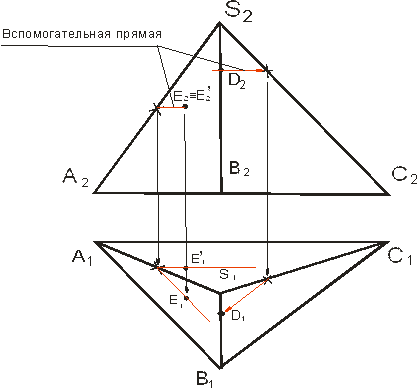
Рисунок 3. Точка на поверхности многогранника.

Точка Е принадлежит боковой поверхности пирамиды (Е₂ задана). По фронтальной проекции нельзя точно сказать, какой грани ASB или АSС, принадлежит точка, поэтому будем рассматривать две конкурирующие точки Е и Е^/. Для построения второй проекции точки Е (Е₁) проводятся вспомогательные прямые, параллельные ребрам основания АС и АВ.

Дата добавления: 2014-01-03