Тогда формула для исчисления реальных средних расстояний примет вид

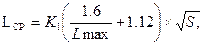
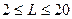
Вычисление средних расстояний в зависимости от размеров зе­мельной площади, соотношения сторон и расположения хозяй­ственного центра подтверждает выводы, сделанные ранее. С уве­личением площади землевладения при прочих равных условиях возрастает и среднее расстояние; этот рост пропорционален кор­ню квадратному площади. Наименьшее среднее расстояние для прямоугольных участков достигается при расположении центра хозяйства в центральной части участка. Среднее расстояние уве­личивается по мере увеличения вытянутости фигур и перемеще­ния хозяйственного центра к границам участка. Только изменени­ем местоположения хозяйственного центра среднее расстояние перевозок может быть увеличено (или уменьшено) более чем в 2

аза, а с учетом соотношения сторон этот разрыв может достигать и больших размеров. Другими словами, увеличение среднего рас­стояния (а значит, и транспортных издержек) может быть связано не только с изменением площади земельного массива. Например, среднее расстояние остается примерно одинаковым для прямоу­гольника в 1000 га с соотношением сторон 1: 5 и размещением хо­зяйственного центра в вершине участка и для массива площадью 9000 га, но имеющего форму квадрата с усадьбой, размещенной в его центре.

Поскольку севообороты и угодья имеют различную грузоем-кость, необходимо учитывать общую площадь, в составе которой находится угодье, до которого определяется среднее расстояние. Например, чтобы определить среднее расстояние до пахотных массивов при 50 % распаханности территории, следует исходить не из площади пашни, а из площади всей территории (то есть в данном случае площадь должна быть увеличена вдвое). Если удельный вес пашни в общей площади снижается, то это приводит к увеличению среднего расстояния транспортировки. Так, с уменьшением удельного веса пашни с 40 до 10 % среднее расстоя­ние возрастает в 3—5 раз.

При неодинаковой грузоемкости одного и того же угодья сред­нее расстояние следует вычислять по формуле

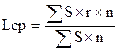
где m — масса грузов, приходящихся на 1 га того или иного участка. r – расстояние передвижения груза

На земельном массиве имеется 2 севооборота: полевой на площади 1500 га (r =4 км, n = 20 т/га) и кормовой на площади 500 га (r=2 км, n = 40 т/га). Тогда среднее расстояние для всего массива, взвешенное по площадям, будет равно

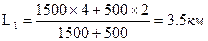
С учетом грузоемкости получим

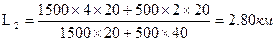
Таким образом, реальное расстояние, вычисленное с учетом грузоемкости, в данном примере существенно (на 20 %) меньше, чем среднее расстояние, взвешенное только по площади.

Если мы разместим кормовой севооборот на большем расстоя­нии (например, 4 км), полевой севооборот приблизится и размес­тится на расстоянии 3,3 км. Среднее расстояние для всего массива при этом не изменится и составит 3,5 км, а среднее расстояние учитывающее грузоемкость, будет равно

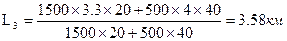
Данный расчет показывает, что для сокращения средних рас­стояний, учитывающих грузоемкость перевозок, грузоемкие куль­туры необходимо приближать к хозяйственным центрам. Тогда и транспортные затраты хозяйства будут гораздо меньше.

Дата добавления: 2014-01-03