Структуры и стратегии поиска в пространстве состояний. Чтобы разрабатывать и внедрять алгоритмы поиска, разработчик должен уметь ана­лизировать и прогнозировать их поведение

Чтобы разрабатывать и внедрять алгоритмы поиска, разработчик должен уметь ана­лизировать и прогнозировать их поведение. При этом перед ним стоят такие вопросы.

Гарантировано ли нахождение решения в процессе поиска?

Является поиск конечным, или в нем возможны зацикливания? Если решение найдено, является ли оно оптимальным?

Как процесс поиска зависит от времени выполнения и используемой памяти? Как интерпретатор может наиболее эффективно упростить поиск?

Как разработать интерпретатор для наиболее эффективного использования языка представления?

Теория поиска в пространстве состояний дает ответы на эти во­просы. Представив задачу в виде графа пространства состояний, можно использовать теорию графов для анализа структуры и сложности как самой задачи, так и процедуры поиска ее решения.

Граф состоит из множества вершин и дуг, соединяющих пары вершин. В модели про­странства состояний решаемой задачи вершины графа представляют дискретные со­стояния процесса решения, например, результаты логического вывода или различные конфигурации игровой доски. Дуги графа описывают переходы между состояниями. Эти переходы соответствуют логическим заключениям или допустимым ходам в игре. Так, в экспертных системах состояния описывают знания о задаче на определенном этапе ис­следования. Экспертные заключения в форме правил "если..., то" позволяют получить новую информацию. При этом каждый случай применения правила представляется как дуга между состояниями.

Теория графов является наилучшим инструментом исследования структуры объектов и их отношений. Именно это и привело к созданию теории графов в начале восемнадцатого века. Швейцарский математик Леонард Эйлер изобрел теорию графов, чтобы решить "задачу о кенигсбергских мостах".

Граф - это множество вершин и дуг между ними. В размеченном графе для каждой вершины задается один или несколько дескрипторов (меток), которые позволяют отли­чить одну вершину графа от другой. На графе пространства состояний эти дескрипторы идентифицируют состояния в процессе решения задачи. Если дескрипторы двух вершин не различаются, то эти вершины считаются одинаковыми. Дуга между двумя вершинами определяется метками этих вершин.

Дуги графа также могут быть размеченными. Метка дуги используется для задания именованного отношения (как в семантических сетях) либо веса дуги (как в задаче о коммивояжере).

Граф называется ориентированным, если каждой дуге приписано определенное на­правление. Дуги в ориентированном графе обычно содержат стрелки, определяющие ориентацию дуги. Дуги, которые можно проходить в любом из двух направлений, могут содержать две стрелки-указателя, но чаще вовсе не имеют стрелок. На рис. 4 изобра­жен размеченный ориентированный граф. По дуге (а,b) можно двигаться лишь от вер­шины а к вершине b, по дуге (b,с) можно двигаться в любом из двух направлений.

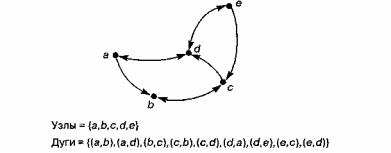
Рисунок 4 - Размеченный ориентированный граф

Путь на графе - это последовательность дуг, соединяющих соседние верши­ны. Путь представляется списком дуг, систематизированным в порядке их следования. На рис.4 список (а,b,с,d) представляет путь, проходящий через вершины а,b,с,d в указанном порядке.

Корневой граф содержит единственную вершину, от которой существует путь к лю­бой вершине графа. Эта вершина называется корнем. При изображении корневого графа корень обычно помещают в верхней части рисунка над всеми остальными верши­нами.

Дерево - это граф, на котором для любых двух вершин существует не более одного пути между ними. Деревья обычно имеют корни, которые изображаются в верх­ней части рисунка, как и для корневых графов. Поскольку для каждой вершины дерева существует не более одного пути в эту вершину из любой другой вершины, то не суще­ствует путей, содержащих петли или циклы.

Для корневых деревьев или графов отношения между вершинами описываются поня­тиями родителя, потомка и вершин-братьев - вершин дерева, имеющих об­щую вершину-родителя. Они используются в обычном смысле наследования: при прохо­де вдоль направленной дуги родитель предшествует потомку. Концы всех направленных дуг, исходящих из одной вершины, называются вершинами-братьями. Аналогично на пути ориентированного графа предок предшествует потомку.

На рис.5 вершина b яв­ляется родителем вершин е и f (которые являются потомками b и вершинами-братьями). Вершины а и с являются предками вершин g, h, i, а вершины g, h, i, являются потомками а и с.

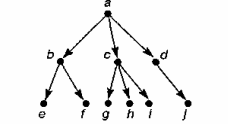
Рисунок 5 - Корневое дерево как пример семейных отношений

Дата добавления: 2014-01-03