Реализация поиска на графах

При решении задач путем поиска на основе данных либо от цели требуется найти путь от начального состояния к целевому на графе пространства состояний. Последова­тельность дуг этого пути соответствует упорядоченной последовательности этапов ре­шения задачи. Модуль решения задачи должен безошибочно двигаться прямо к цели, запоминая путь движения. Решатель дол­жен рассматривать различные пути до тех пор, пока не достигнет цели. Поиск с возвра­тами - это метод систематической проверки различных путей в про­странстве состояний. Это один из пер­вых алгоритмов поиска в информатике.

Алгоритм поиска с возвратами запускается из начального состояния и следует по некото­рому пути до тех пор, пока не достигнет цели либо не упрется в тупик. Если цель достигнута, поиск завершается, и в качестве решения задачи возвращается путь к цели. Если же поиск привел в тупиковую вершину, то алгоритм возвращается в ближайшую из пройденных вер­шин и исследует все ее вершины-братья, а затем спускается по одной из ветвей, ведущих от вершины-брата. Этот процесс описывается следующим рекурсивным правилом.

Алгоритм работает до тех пор, пока не достигнет цели либо не исследует все про­странство состояний. На рис.7 изображен процесс поиска с возвратами в гипотети­ческом пространстве состояний.

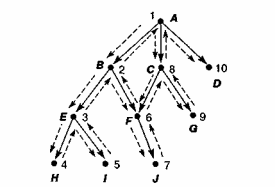
Рисунок 7 - Поиск с возвратами в гипо­тетическом пространстве состояний

Пунктирные стрелки в дереве указывают направление процесса поиска в пространстве состояний (вниз или вверх). Числа возле каждой верши­ны указывают порядок их посещения. Ниже приведем фрагмент алгоритма поиска с возвратами. В нем используются три списка, позволяющих запоминать путь от узла к узлу в про­странстве состояний.

SL (State List) - список исследованных состояний рассматриваемого пути. Если цель уже найдена, SL содержит список состояний пути решения.

NSL (New State List) - список новых состояний, он содержит вершины, подлежащие рассмотрению, т.е. список вершин, потомки которых еще не были порождены и рас­смотрены.

DЕ (Dead Ends) - список тупиков, т.е. список вершин, потомки которых уже были ис­следованы, но не привели к цели. Если состояние из этого списка снова встречается в процессе поиска, то оно обнаруживается в списке DЕ и исключается из рассмотрения.

При описании алгоритма поиска с возвратами на графах общего вида (не только для деревьев) необходимо учитывать возможность повторного появления состояний, чтобы избежать их повторного рассмотрения, а также петель, ведущих к зацикливанию алго­ритма поиска пути. Это обеспечивается проверкой каждой вновь порожденной вершины на ее вхождение в один из трех вышеуказанных списков. Если новое состояние обнару­жится хотя бы в одном из двух списков SL или DE, значит, оно уже рассматривалось, и его следует проигнорировать.

Обозначим текущее состояние при поиске с возвратами через CS (current state). Со­стояние CS всегда равно последнему из состояний, занесенных в список SL, и представ­ляет "фронтальную" вершину на построенном в данный момент пути. Правила вывода, ходы в игре или иные соответствующие операторы решения задачи упорядочиваются и применяются к CS. В результате возникает упорядоченное множество новых состояний, потомков CS. Первый из этих потомков объявляется новым текущим состоянием, а ос­тальные заносятся в список новых состояний NSL для дальнейшего изучения. Новое те­кущее состояние заносится в список состояний SL, и поиск продолжается. Если текущее состояние CS не имеет потомков, то оно удаляется из списка состояний SL (именно в этот момент алгоритм "возвращается назад"), и исследуется какой-либо из оставшихся потомков его предка в списке состояний SL.

Алгоритм поиска с возвратами на графе из рис.7 работает следующим образом.

Инициализируем списки.

Поиск с возвратами в данном случае является поиском на основе данных, при кото­ром корень дерева связывается с начальным состоянием, а потомки узлов анализируются для построения пути к цели. Этот же алгоритм можно интерпретировать и как поиск от цели. Для этого целевую вершину следует взять в качестве корня дерева и анализировать совокупность предков для нахождения пути к начальному состоянию.

Поиск с возвратами - это алгоритм поиска на графе пространства состояний. Алгоритмы поиска на графах, которые будут рассматриваться далее, включая поиск в глубину, поиск в ширин, используют идеи поиска с возвратами, в том числе следующие.

1.Формируется список неисследованных состояний (NSL), для того чтобы иметь возможность возвратиться к любому из них.

2.Поддерживается список "неудачных" состояний (DE), чтобы оградить алгоритм от проверки бесполезных путей.

3.Поддерживается список узлов (SL) текущего пути, который возвращается по дос­тижении цели.

4.Каждое новое состояние проверяется на вхождение в эти списки, чтобы предотвратить зацикливание.

В следующем подразделе рассматриваются алгоритмы с использованием списков, по­добные алгоритму поиска с возвратами. Эти алгоритмы, среди которых поиск в глубину, поиск в ширину, отличаются от по­иска с возвратами более гибкими средствами и стратегиями поиска.

Дата добавления: 2014-01-03