Сравнение стратегий поиска

Поиск в глубину

Этот вид поиска противоположен поиску в ширину. Поиск в глубину (рис.9) просматривает одно направление до тех пор, пока его вершины не исчерпаются или пока не будет достигнута цель. Проблема заключается в том, что при этом поиске при неизвестной глубине может возникнуть потребность в некотором останавливающем правиле.

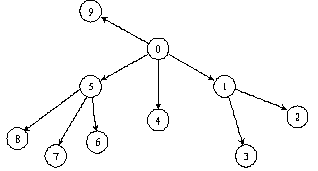
Рисунок 9 – Дерево поиска в глубину

Сравним поиск в глубину и в ширину на примере.

Рассмотрим в качестве примера задачу построения слова из некоторого множества букв. Задавшись набором операций установки букв, можно сформировать пространство состояний..

Предположим, что множество доступных букв включает P = {К, Т, О}. На каждом уровне графа мы будем добавлять по одной определенной букве. Каждая ветвь, исходящая из узла, соответствует установке буквы в определенную позицию в последовательности, а эта последовательность должна образовать осмысленное слово. Если это про­изошло, то головоломка считается собранной. Целью работы будет построить все распознаваемые человеком последовательности и найти слово КОТ.

Примем за начальную точку – O. Дерево пространства состояний (неизменно) рис.10:

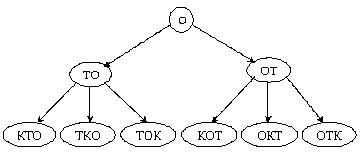
Рисунок 10 – Дерево пространства состояний

Метод формирования, анаграмм последовательным перечислением является приме­ром применения алгоритма, получившего наименование generate-and-test (порождение и проверка).

1. Генерировать новое состояние, модифицируя существующее; например, изменитьоследовательность букв, добавив новую в существующую последовательность.

2. Проверить, не является ли образовавшееся состояние конечным (решением); на­пример, проверить, не является ли образовавшаяся последовательность осмыслен­ным словом. Если это так, то завершить, иначе перейти к шагу (1).

Алгоритм имеет два основных варианта: поиск в глубину и поиск в ширину. Отличаются варианты порядком формирования состояний на шаге (1).

Алгоритм поиска в ширину - сначала формируются все "соседи" узла N, а потом уже строятся его потомки. Таким образом, в алгоритме поиска в ширину просматриваются последовательно состояния, представлен­ные узлами одного и того же уровня на графе. Дерево решений при использовании поиска в ширину:

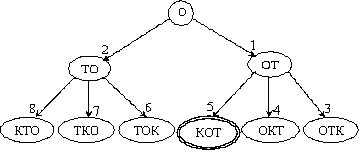
Рисунок 11 – Дерево решений при использовании поиска в ширину

Алгоритм поиска в глубину. Для любого данного узла N алгоритм поиска в глубину строит потомок этого узла, т.е. формирует состояние, которое образуется в результате применения операторов к уз­лу N, а потом переходит к формированию узла, ближайшего к N, на том же уровне графа ("соседу" N), т.е. формирует состояние, которое образуется в результате применения оператора к узлу-родителю N.

Дерево решений при использовании поиска в глубину:

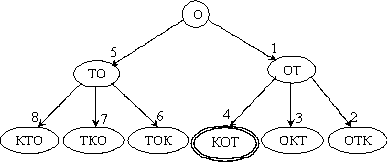
Рисунок 12 – Дерево решений при использовании поиска в глубину

Алгоритм поиска в ширину отыскивает решение, путь к которому кратчайший, если оно существует (это кратчайший путь между исходным состоянием и решением). Алгоритмы, обладающие такими свойствами, называются разрешимыми.

Поиск в глубину может быстрее найти решение, особенно если используются эвристики для выбора очередной ветки, но алгоритм может никогда не закончиться, если пространство состояний неограниченно. Оба алгоритма завершат работу (найдут конечное состояние) после формирования узла «кот». Но алгоритму поиска в ширину придется для этого "посетить" пять узлов (сформировать и проанализировать пять состояний), а алгоритму поиска в глуби­ну - четыре.

Нетрудно заметить, что число узлов растет экспоненциально по мере увеличения числа уровней на графе. Это явление часто называют комбинаторным взрывом, и оно представляет очень серьезную проблему при программировании таких задач, например при "грубом" переборе всех возможных вариантов позиций в игре в шахматы. Поскольку человеческий мозг слабее компьютера при решении задач, связанных с перебором вариантов, естественно предположить, что серьезный шахматист решает эту задачу каким-то другим способом. Скорее всего, он использует свой опыт, воображение и аналитические способности, во-первых, для формирования общей стратегии игры, а во-вторых, для выбора наилучшего очередного хода. Вот такой-то способ решения мы и на­зываем "интеллектуальным".

Дата добавления: 2014-01-03