Построение дерева решений сверху вниз

Согласно алгоритму ID3 дерево решений строится сверху вниз. Заметим, что каждое свойство позволяет разбить набор обучающих примеров на непересекающиеся подмножества каждому из которых относятся все примеры с одинаковым значением этого множества. Но алгоритму ID3 каждый узел дерева представляет некоторое свойство, на основании которого выполняется разделение выбора примеров. Таким образом, алгоритм рекурсивно строит поддерево для каждого раздела. Эта процедура длится до тех пор, пока все элементы раздела не будут отнесены к одному и тому же классу. Этот класс становится конечным узлом дерева. Поскольку для построения простого дерева решении важную роль играет порядок тестирования, в алгоритме ID3 реализован специальный критерий выбора теста для корневого узла каждого поддерева. Чтобы упростить описание, рассмотрим алгоритм построения деревьев решении в предположении, что существует соответствующая функция выбора.

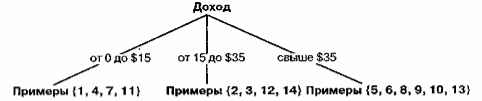Например, рассмотрим процесс построения дерева, представленного на рисунке 14 на основе данных из таблицы 1. Имея полную таблицу примеров, алгоритм ID3 выбирает в качестве корневого свойства значение дохода на основе функции выбора. При этом множество примеров делится на три части, как показано на рисунке 15. Элементы каждой части представлены порядковыми номерами примеров в таблице.

Рисунок 15 - Упрощенное дерево решений для оценки кредитного риска

Алгоритм индукции начинает свою работу с отбора корректно классифицированных элементов целевых категорий. Алгоритм строит дерево решений следующим образом:

Function induce_tree (example_set, Properties)

Begin

если все элементы набора примеров example_set принадлежат к

одному и тому же классу,

то вернуть конечный узел,

отнеся его к этому классу, иначе, если множество Properties пусто,

то вернуть конечный узел, именем которого является объеденение всех

имен классов в example_set

иначе Begin

выбрать свойство Р и назначить его корнем

текущего дерева;

удалить свойство Р из множества Properties для каждого

значения V свойства Р

Begin

создать ветвь дерева с меткой V;

к разделу partition отнести

элементы множества example_set, для которых свойство Р

принимает значение V;

вызвать функцию induce_tree ( partition_v Properties ), добавить

результаты к ветви V

Cогласно алгоритму функция induce_tree рекурсивно вызывается для каждого раздела. Например, пусть к разделу {1,4,7,11} относятся клиенты с высоким риск­ом; алгоритм создаст соответствующий конечный узел. Затем в качестве корневого узла поддерева раздела {2, 3, 12, 14} выбирается свойство "кредитная история". На рисунке 16 элементы этого раздела в свою очередь разбиваются на три группы: {2, 3}, {14} и {12}.

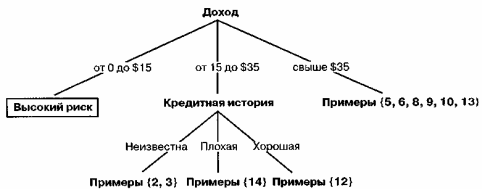
Рисунок 16 - Фрагмент дерева решений

Таким образом, строится дерево, представленное на рисунке 14. Оставшуюся часть дерева предлагается построить самостоятельно. Набор всех возможных деревьев решений можно рассматривать как пространство версий. Операции перемещения в этом пространстве соответствуют добавлению частей дерева. Алгоритм реализует вариант поиска по первому наилучшему совпадению в пространстве всех возможных деревьев. Он добавляет дерево к текущему поддереву и продолжает поиск, не возвращаясь к исходной точке. Это обеспечивает высокую эффективность алгоритма, а также зависимость от критерия выбора свойств.

Дата добавления: 2014-01-03