Распределение Максвелла

Закон распределения по скоростям молекул газа, находяще­гося в термодинамическом равновесии, был найден Максвел­лом году.

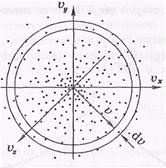
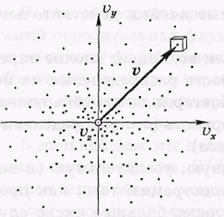Следствие того, что все направления x,y,z-равновестны и равноправны расположил кол-во точек.

Пусть газ содержит – N молекул

dx,dy,dz – малый объем.

Относительное число.

Под Dn-понимает среднее число молекул в соответствующем интервале той или иной велечины.

Функция f(v) имеет смысл объемной плотности вероятности.

Вероятность того что молекула будет иметь проекции скорости в интервале (Vx,Vx+dVx) есть

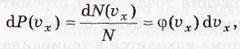
Это выражение относительно число молекул в тонкой плоскости им величины.

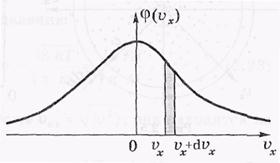
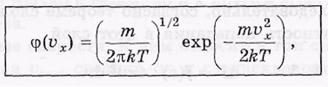
Exp-экспамент.

Распределение молекул по модулю скорости.Найдем вероятность или относительное число молекул, мо­дуль скорости которых заключен в интервале (v, v + dv).

Распределения Максвелла по модулю скорости.

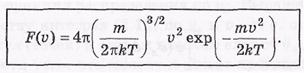
С помощью этой формулы можно находить число молекул скорости которых лежат в заданном интервале скоростей.

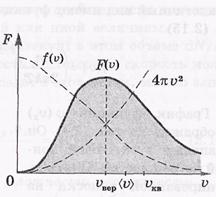
Распределение Максвелла по скоростям не зависит от структуры молекул, ни от того как они взаимодействуют друг с другом, поэтому распределение Максвелла применимо не только к газам но и другим агрегатным состояниям вещества.

Характерные скорости.

1)наболее вероятная

2) средняя

3) средняя квадатичная.

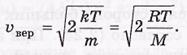
Средняя скорость по определению

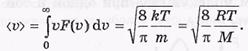
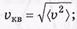Среднеквадратичная скорость она находится из условия

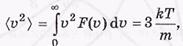
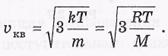откуда следует, что

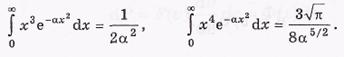
Скорость молекулы Азота при 300 по К составляет порядка 480м/c

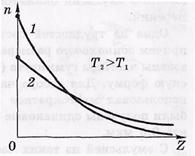
Зависимость распределения от температуры

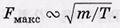
Формула Максвелла в приведенном виде.

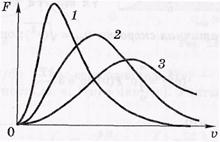
Функции распределения Ф(ε) молекул по их кинетич. энергииям Е поступательного движения.

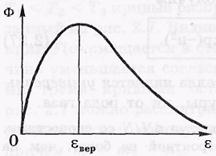
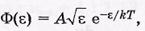
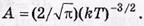
Dф/d Е=0,то Евер=KT/2

Распределение Больцмана.

В отсутствие внешних сил средняя концентрация п молекул газа в состоянии термодинамического равновесия всюду одина­кова. Если же газ находится во внешнем силовом поле, концентрация молекул описывается распределением Больцмана.

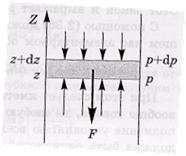
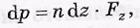
где F_z — проекция силы.

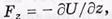
:потенциальная энергия

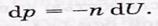
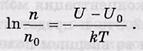
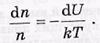интегрируем-

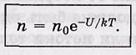
-(Uэл.пот,KT-энер.темп.движения)

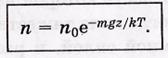
Распределение Больцмана показывает что в распределение молекул силы тяжести и тепловое движение.

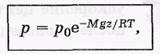
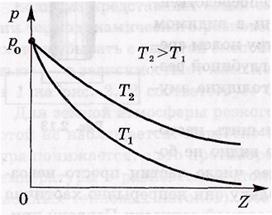
Барометрическая формула давление уменьшает при поъеме по закону показ.функции.

также, что с высотой темпера­тура понижается, а это противоречит требованию одинаковости температуры в равновесном столбе газа (во избежание конвек­ционных тепловых потоков). Все это указывает на то, что зем­ная атмосфера не находится в состоянии статистического рав­новесия.

Дата добавления: 2014-01-03