Потери напора при ламинарном течении жидкости

Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.4.3).

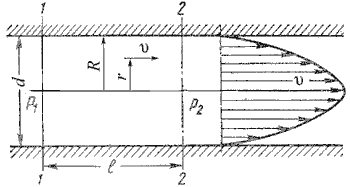
Рис. 4.3. Схема для рассмотрения ламинарного потока

Уравнение, связывающее переменные υ и r, имеет следующий вид:

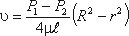
где P1 и P2 - давления соответственно в сечениях 1 и 2.

У стенок трубы величина r = R,, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной

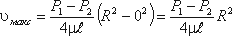
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.

Максимальная скорость дает высоту параболоида

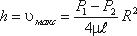
Как известно из геометрии, объем параболоида высотой h и площадью ρ R ² равен

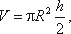
а в нашем случае

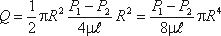
Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид

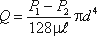
Расход в трубе можно выразить через среднюю скорость:

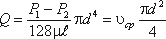
откуда

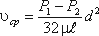
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).

Потеря давления в трубопроводе будет равна

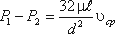
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ (μ = υ ρ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:

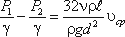
Так как левая часть полученного равенства равна потерям напора h_пот в трубе постоянного диаметра, то окончательно это равенство примет вид:

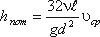
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:

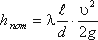
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:

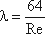
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу

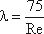
Дата добавления: 2014-01-03