Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

С ледствием из интегральной теоремы Муавра-Лапласа является формула для вычисления вероятности осуществления неравенства

,

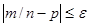то есть вероятности того, что отклонение относительной частоты m/n наступления события А от его вероятности p не превышает по абсолютной величине некоторого заданного числа e:

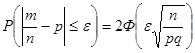. (11.1)

Равенство (11.1) легко выводится из (10.1) и носит название формулы вероятности отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

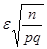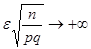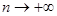Заметим, что при достаточно большом числе испытаний n и фиксированном e величина тоже велика ( при ), и 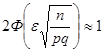(поскольку при x > 5 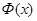»0,5). Это означает, согласно (11.1), что

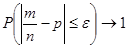при 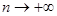. (11.2)

Соотношение (11.2) носит название теоремы Бернулли. Оно показывает, что при достаточно большом числе испытаний n практически достоверным можно считать тот факт, что отклонение относительной частоты m/n (т.е. статистической вероятности) наступления события А от его вероятности p не превышает по абсолютной величине любого сколь угодно малого заданного числа e.

Практически равенство (11.2) означает следующее: при большом числе испытаний n статистическая вероятность события m/n приближается к его классической вероятности p, т.е. 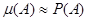. Подбрасывая монету достаточно большое число раз, мы вправе ожидать, что герб будет выпадать примерно в половине случаев. Бросая кубик достаточно большое число раз, можно ожидать, что шестерка выпадет в 1/6 части опытов и т.д.

Дата добавления: 2014-01-03