Теорема Остроградського-Гаусса

Перед розглядом цієї теореми слід зробити деякі попередні зауваження.

Хоча закон Кулона і принцип суперпозиції полів дають можливість визначати вектор напруженності електричного поля будь-якої системи зарядів, проте це пов'язано з досить громіздкими обчисленнями. Для спрощення цієї задачі слід скористатись деякими теоремами про загальні властивості електростатичного поля, однією з яких і є теорема Остроградського-Гаусса, яка дає можливість відмовитись від теорії далекодії (саме на ній базується закон Кулона) і звести рівняння електростатики до диференціальної форми і, таким чином, узгодити їх з теорією близькодії.

Теорема Остроградського-Гаусса пов'язує потік вектора (або вектора 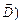крізь довільну замкнену поверхню з зарядом, який охоплюється цією поверхнею. Для виведення цієї теореми слід ввести поняття потоку.

Потік вектора . Число ліній напруженості електричного поля , що пронизують елементарну площадку d S, дорівнює

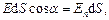
де 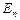– проекція вектора на нормаль 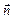до площадки d S (рис. 1).

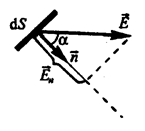
Рис. 1

Величина

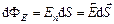
– це потік вектора напруженості крізь площадку d S, 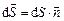– вектор, модуль якого дорівнює d S, а напрям вектора співпадає з напрямом нормалі 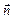до площадки.

Потік вектора крізь довільну замкнену поверхню S:

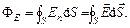
Потік вектора – це алгебраїчна величина (залежить від конфігурації поля і від вибору напряму ).

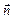Теорема Остроградського-Гауса для електростатичного поля у вакуумі

Потік вектора крізь сферичну поверхню радіусу r дорівнює:

.

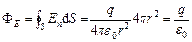Цей результат справедливий для замкненої поверхні будь-якої форми. Так, якщо оточити сферу (див. рис. 2) довільною замкненою поверхнею, то кожна лінія напруженості, яка пронизує сферу, пройде і крізь цю поверхню.

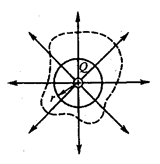
Рис. 2

Загальний випадок: довільна поверхня, що охоплює n зарядів. Відповідно до принципу суперпозиції напруженість поля, створюваного всіма зарядами, дорівнює сумі напруженостей 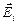, створюваних кожним зарядом окремо: = 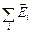. Тому неважко показати, що

.

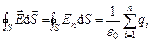Теорема Остроградського-Гаусса для поля у вакуумі. Потік вектора напруженості електростатичного поля у вакуумі крізь довільну замкнуту поверхню дорівнює алгебраїчній сумі поміщених усередині цієї поверхні зарядів, ділених на :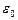

.

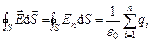Якщо заряд розподілений в просторі з об'ємною густиною 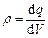,то теорема Остроградського-Гауса для електростатичного поля у вакуумі матиме вид:

.

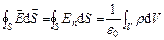Застосування теореми Остроградського-Гаусса до розрахунку полів у вакуумі

1. Поле рівномірно зарядженої нескінченної площини

Нескінченна площина заряджена з постійною поверхневою густиною 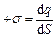(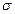– заряд, що припадає на одиницю поверхні). Лінії напруженості перпендикулярні даній площині і направлені від неї в обидві сторони. В якості замкненої поверхні подумки побудуємо циліндр, основи якого паралельні зарядженій площині, а вісь перпендикулярна їй (рис. 3). Повний потік крізь циліндр дорівнює сумі потоків крізь його основи (площі основ однакові і для основи 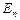співпадає з Е), тобто дорівнює 2 ES. Згідно з теоремою Остроградського-Гаусса, 2 ES = =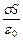, звідки

.

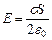Цей результат свідчить про те, що напруженість 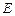не залежить від довжини циліндра і на будь-яких відстанях від площини напруженість 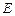однакова за величиною. Картина ліній напруженості 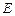наведена на рис.

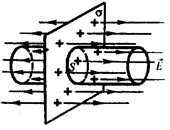
Рис. 3

2. Поле рівномірно зарядженої сферичної поверхні

Сферична поверхня радіусу R із загальним зарядом 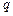заряджена рівномірно з поверхневою густиною .

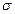Завдяки рівномірному розподілу заряду по поверхні створюване цим зарядом поле має сферичну симетрію. Тому лінії напруженості направлені радіально (рис. 4, а).

Побудуємо подумки сферу радіусу 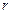, яка має спільний центр із зарядженою сферою. Якщо 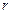> R, то всередину поверхні потрапляє весь заряд 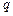, що створює дане поле, і, по теоремі Остроградського-Гаусса,

,

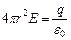звідки

.

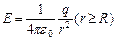При 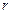> R поле спадає з відстанню 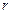по такому ж самому закону, що і для точкового заряду. Графік залежності Е від 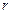наведено на рис. 4, б. Якщо 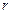' < R, то замкнена поверхня не містить усередині зарядів, тому всередині рівномірно зарядженої сферичної поверхні Е = 0.

Рис. 4

3. Поле об'ємно зарядженої кулі

Куля радіусу R із загальним зарядом 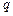заряджена рівномірно з об'ємною густиною 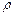(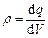– заряд, що припадає на одиницю об'єму). Внаслідок симетрії для напруженості поля ззовні кулі матимемо той же результат, що і у разі сферичної поверхні:

.

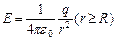Усередині кулі напруженість інша. Сфера радіусу 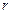'< R охоплює заряд .

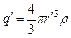Тому, згідно з теоремою Остроградського-Гаусса,

.

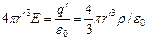Враховуючи, що

,

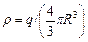отримаємо

.

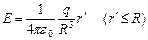Графік залежності Е від 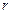наведено на рис. 5.

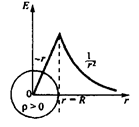
Рис. 5

4. Поле рівномірно зарядженого нескінченного циліндра (нитки)

Нескінченний циліндр радіусу R заряджений рівномірно з лінійною густиною 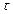(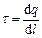– заряд, що припадає на одиницю довжини). Внаслідок симетрії лінії напруженості поля будуть направлені по радіусах кругових перерізів циліндра з однаковою густиною у всі сторони відносно осі циліндра. В якості замкненої поверхні подумки побудуємо коаксіальний із зарядженим циліндр радіусу 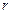і висотою 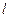. Потік вектора Е крізь торці циліндра дорівнює нулю (торці паралелі лініям напруженості), а крізь бічну поверхню 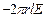. По теоремі Остроградського-Гаусса при 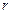> R

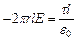
звідки

.

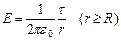Якщо 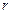< R, то замкнена поверхня всередині не містить зарядів, і тому в цій області Е = 0.

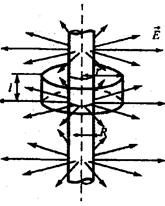
Рис. 6

******************************************************************

Принцип суперпозиції. Поле диполя

Принцип суперпозиції (накладення) електростатичних полів

Напруженість Е результуючого поля, створюваного системою зарядів, рівна геометричній сумі напряженностей полів, створюваних в даній крапці кожним із зарядів окремо.

Електричний диполь

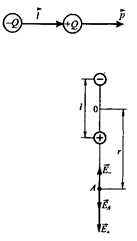
Система двох рівних по модулю різнойменних точкових зарядом (+& -0. відстань / між якими значно менше відстані до даних точок поля.

Плече диполя

Вектор, направлений по осі диполя (прямої, що проходить через оОа заряду) від негативного заряду до позитивного і рівні і відстані між ними.

Електричний момент диполя ______

Вектор

W

співпадаючий по напряму з плечем диполя.

-H+0J

За принципом суперпозиції, напруженість поля диполя. в довільній крапці Е = Е+ + Е_ (Е+ і?_ — напруженості полів, створюваних відповідно позитивним і негативним зарядами).

Напруженість поля на продовженні осі диполя в крапці А

**********************************

ЛЕКЦІЯ 06

Діелектрики в електричному полі

Термін "діелектрик" (від гр. 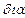– через, крізь і англ. еlесtrіс – електричний) вперше ввів М. Фарадей у 1837 р. для характеристики речовин, в які проникає електричне (електромагнітне) поле. Зазвичай під діелектриками розуміють речовини, крізь які практично погано проходить електричний струм, а в ідеальному випадку – зовсім не проходить. Це зумовлено внутрішньою будовою атомів і молекул діелектриків і, насамперед, відсутністю в них таких зарядів, які б могли під дією поля вільно переміщатись на макроскопічні відстані.

Діелектрики являють собою електрично нейтральні системи: їх сумарний позитивний заряд, яких зосереджений у ядрах, і негативний заряд в електронних шарах довільного об'єму діелектричної речовини однакові.

За характером просторового розміщення заряджених часток у молекулах діелектрики поділяють на неполярні і полярні.

Діелектрики з неполярними молекулами (наприклад, гази N₂, Н₂, О₂, СО₂) – це діелектрики, які мають симетричну будову, тобто у них "центри ваги" позитивних і негативних зарядів за відсутності електричного поля збігаються і, отже, дипольний момент молекул дорівнює нулю.

Діелектрики з полярними молекулами (наприклад, гази СО, Н₂О, NН₃, SО₂) – це діелектрики, молекули яких за відсутності електричного поля мають дипольні моменти 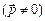, які внаслідок теплового руху зорієнтовані в просторі хаотично і їхній результуючий момент дорівнює нулю.

Іонні діелектрики (наприклад, NaС1, КС1) – це тверді діелектрики, іонні кристали яких є просторовими гратами з правильним чергуванням іонів різних знаків.

Можлива також класифікація діелектриків за типом симетрії і за властивостями структурних одиниць, з яких діелектрик складається (наприклад, рис. 6.1: а – монопольні, б – дипольні, в – квадрупольні, г – октупольні та ін.).

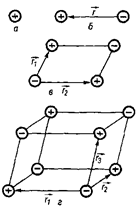
Рис. 6.1

Ні одній із класифікацій діелектриків не можна надати переваги, оскільки жодна з них не є універсальною.

2. Поляризація діелектриків. Вектор поляризації

Для діелектриків характерною є особлива їх поведінка у зовнішньому електричному полі – поляризація. Поляризація – це процес орієнтації диполів чи поява під дією електричного поля орієнтованих по полю диполів.

Відповідно до трьох вище наведених груп діелектриків (з неполярними молекулами, з полярними молекулами, іонні діелектрики) розрізняють три види поляризації:

1) електронну (деформаційну), – характерну для діелектриків з неполярними молекулами, яка полягає у виникненні у атомів індукованого дипольного моменту за рахунок деформації електронних орбіт;

2) орієнтаційну (дипольну), – характерну для діелектриків з полярними молекулами, яка полягає в орієнтації наявних дипольних моментів по полю. Ця орієнтація тим сильніша, чим більша напруженість електричного поля і чим нижча температура;

3) іонну поляризацію діелектриків з іонними кристалічними ґратками, яка полягає у зміщенні підрешітки позитивних іонів вздовж поля, а негативних – проти поля, що призводить до виникнення дипольних моментів.

Розглянемо тепер таке поняття, як поляризованість.

Поляризованість – це векторна величина, яка визначається дипольним моментом одиниці об'єму діелектрика:

,

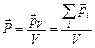де 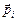– дипольний момент однієї молекули.

Дослідні дані свідчать, що для великого класу ізотропних діелектриків (крім сегнетоелектриків) поляризованість 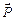лінійно залежить від напруженості електричного поля :

,

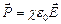де 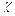– стала, яку називають діелектричною сприйнятливістю діелектрика.

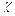– величина безрозмірна, притому 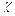> 0 для більшості діелектриків (наприклад, для спирта 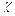= 25, для води 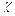= 80).

Для встановлення кількісних закономірностей поля в діелектрику внесемо пластину з однорідного діелектрика в однорідне електричне поле, створене двома нескінченними разнойменно зарядженими площинами, розмістивши її так, як показано на рис. 6.2.

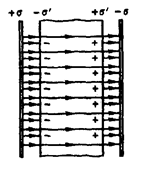
Рис. 6.2

Під дією поля діелектрик поляризується, тобто в ньому відбувається зміщення зарядів: позитивні заряди зміщуються по полю, негативні – проти поля. В результаті цього на правій грані діелектрика, оберненого до площини з негативними зарядами, буде надлишок позитивних зарядів з поверхневою густиною +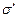, а на лівій – від'ємного заряду –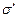. Ці нескомпенсовані заряди, які з'явились в результаті поляризації діелектрика, називаються зв'язаними зарядами, причому 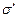< 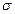. Поле зв'язаних зарядів 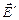спрямовано проти зовнішнього поля (тобто, проти поля, створюваного вільними зарядами 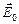) і послаблює його. Результуюче поле всередині діелектрика:

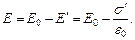(1)

Визначивши поверхневу густину зв'язаних зарядів 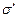= Р (оскільки, з одного боку 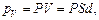де 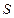– площа грані пластинки; 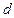– її товщина; а з іншого боку 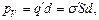тобто 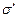= Р) і підставивши в формулу (1) значення 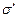, матимемо:

.

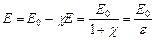Безрозмірна величина

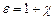
називається діелектричною проникністю середовища. Вона показує, у скільки разів поле послаблюється діелектриком і таким чином кількісно характеризує властивість діелектрика поляризуватись в електричному полі.

Розглянемо тепер поняття електричного зміщення. Напруженість електростатичного поля, як щойно було доведено, залежить від властивостей середовища (в однорідному ізотропному середовищі Е ~ 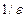). Вектор , переходячи через границю діелектриків, терпить скачкоподібне змінювання, створюючи тим самим незручності під час розрахунків електростатичних полів. Тому виявилось, що крім вектора напруженості електричного поля необхідно ввести ще нову величину – вектор електричного зміщення

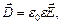або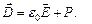

Одиниця електричного зміщення – Кл/м².

3. Лінії електричного зміщення і потік електричного зміщення.

Звернемо увагу на такі поняття, як лінії електричного зміщення і потік електричного зміщення.

Лінії електричного зміщення – це лінії, дотичні до яких в кожній точці співпадають з напрямком вектора 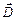. Напрям і густоту цих ліній визначають так само, як і для ліній вектора . Лінії вектора можуть починатись і закінчуватись на будь-яких зарядах – вільних і зв'язаних; в той же час лінії вектора 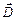– лише на вільних зарядах. Через області поля, де знаходяться зв'язані заряди, лінії вектора 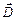проходять не перериваючись.

Потік електричного зміщення для замкненої поверхні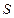

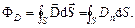
4. Теорема Остроградського-Гаусса для електростатичного поля в діелектриці

Теорема Остроградського-Гаусса для електростатичного поля в діелектриці має вид:

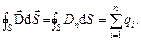
тобто потік вектора електричного зміщення крізь довільну замкнену поверхню дорівнює алгебраїчній сумі всіх вільних електричних зарядів, розташованих всередині поверхні.

Ця теорема справджується як для однорідного і ізотропного, так і для неоднорідного і анізотропного середовища.

5. Сегнетоелектрики, їх властивості та використання

Сегнетоелектрики – це діелектрики, що мають в певному інтервалі температур спонтанну (мимовільну) поляризованість, тобто поляризованість у відсутності зовнішнього електричного поля. До сегнетоелектриків відносяться, наприклад, детально вивчені І. В. Курчатовым і П. П. Кобеко сегнетова сіль, від якої і отримали свою назву сегнетоелектрики, і титанат барія.

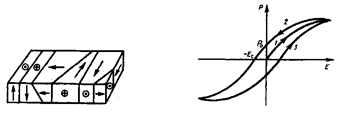
За відсутності зовнішнього електричного поля сегнетоелектрик є мов би мозаїкою з доменів – областей з різними напрямами поляризованої. Це схематично показано на прикладі тнтаната барія (рис. 6.3, а), де стрілки і знаки: крапка в кружечку і плюс в кружечку вказують напрям вектора 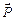. Оскільки в суміжних доменах ці напрями різні, то в цілому дипольний момент діелектрика дорівнює нулю. При внесенні сегнетоелектрика в зовнішнє поле відбувається переорієнтація дипольних моментів доменів по полю, а виникле при цьому сумарне електричне поле доменів підтримуватиме їх деяку орієнтацію і після припинення дії зовнішнього поля. Тому сегнетоелектрики мають аномально великі значення діелектричної проникності (для сегнетової солі, наприклад ).

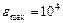Сегнетоелектричні властивості сильно залежать від температури. Для кожного сегнетоелектрика є певна температура, вище за яку його незвичайні властивості зникають і він стає звичайним діелектриком. Ця температура називається точкою Кюрі. Як правило, сегнетоелектрики мають тільки одну точку Кюрі; виняток становлять лише сегнетова сіль (–18 і +24°С) і ізоморфні з нею з'єднання.

Діелектрична проникність 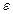(а отже, і діелектрична сприйнятливість 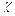сегнетоелектриків залежить від напруженості поля в речовині.

Для сегнетоелектриків формула 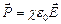не справджується; для них зв'язок між векторами поляризованності (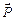) і напруженості поля () нелінійна і залежить від значень в попередні моменти часу. В сегнетоелектриках спостерігається явище діелектричного гістерезису ("запізнювання"). Як видно з рис. 6.3, б із збільшенням напруженості зовнішнього електричного поля поляризованість 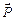зростає, досягаючи насичення (крива 1). Зменшення 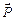із зменшенням відбувається по кривій 2, і при Е = 0 сегнетоелектрик зберігає залишкову поляризованість 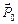, тобто сегнетоелектрик залишається поляризованим у відсутності зовнішнього електричного поля. Для знищення залишкової поляризованості треба прикласти електричне поле зворотного напряму 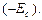Величина 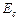називається коерцитивною силою (від лат. соеrticio – утримування). Подальше змінювання 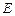призводить до того, що Р змінюється по кривій 3 петлі гістерезису.

В наш час відомо більше 100 сегнетоелектриків, не рахуючи твердих розчинів. Сегнетоелектрики широко застосовуються як матеріали з великим значенням 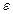(наприклад, в конденсаторах).

а б

Рис. 6.3

ЛЕКЦІЯ 07

Провідники в електричному полі

1. Напруженість поля всередині провідника. Різні тіла ведуть себе по різному в зовнішньому електричному полі: в діелектриках заряджені частинки перебувають у зв'язаному стані і тому під дією електричного поля відбувається лише їх невелике зміщення; в провідниках (металах, електронних напівпровідниках, електролітах, іонізованих газах) заряджені частинки під дією зовнішнього поля можуть вільно переміщуватись. Рух заряджених частинок провідника, внесеного в постійне зовнішнє електростатичне поле, яке створюється сторонніми нерухомими зарядами, викличе появу струму. Проте цей рух має обов'язково припинитись, оскільки провідник, поміщений в електричне поле, можна було б використати для побудови вічного двигуна першого роду. Дійсно, це неможливо, оскільки в противному разі в провіднику виник би упорядкований рух зарядів без затрати енергії від зовнішнього джерела, що протирічить закону збереження енергії.

Рух зарядів в провіднику відбуватиметься лише протягом дуже короткого часу, а саме: доти, доки не встановиться рівновісний розподіл зарядів, за якого електростатичне поле всередині провідника перетвориться в нуль. Таким чином, напруженість електричного поля у всіх точках всередині провідника дорівнює нулю:

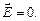
Заряди розміщуються лише на поверхні провідника.

2. Еквіпотенціальність провідника. Оскільки всередині провідника 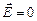, то це означає, що потенціал у всіх точках всередині провідника постійний (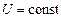), тобто поверхня провідника в електростатичному полі є еквіпотенціальною. Звідси ж таки витікає, що вектор на зовнішній поверхні провідника направлений по нормалі до кожної точки його поверхні. Якби це було не так, то під дією 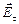заряди почали б переміщуватись по поверхні провідника, що протирічить рівновісному розподілу зарядів.

3. Зв'язок між вектором Е поблизу провідника і 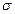. Знайдемо взаємозалежність між вектором поблизу поверхні зарядженого провідника і поверхневою густиною 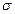зарядів на його поверхні. Для цього застосуємо теорему Остроградського-Гаусса до нескінченно малого циліндра з основою 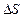, який перетинає границю провідник – діелектрик, і ось якого зорієнтована вздовж вектора (рис. 7.1)

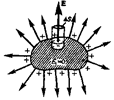
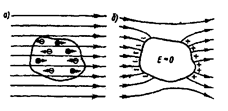
Рис. 7.1 Рис. 7.2

Потік вектора електричного зміщення через внутрішню частину циліндричної поверхні дорівнює нулю, оскільки всередині провідника Е = D = 0, і тому потік вектора 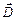через замкнену циліндричну поверхню визначається лише потоком через зовнішню основу циліндра. Згідно з теоремою Гаусса для електростатичного поля в діелектриці

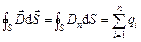
цей потік (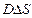) дорівнює сумі зарядів 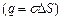, що охоплюються циліндричною поверхнею: 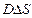=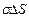, тобто

=

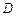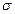
або

,

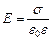де 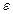– діелектрична проникність середовища, яке оточує провідник.

Можна показати, що це співвідношення визначає Е електростатичного поля поблизу поверхні провідника будь-якої форми.

Електростатична індукція

З'ясуємо, що саме відбудеться, якщо незаряджений провідник внести в задане електростатичне поле, яке створюється якими-небуть сторонніми нерухомими зарядами. В провіднику, внесеному в таке поле, повинні виникнути вільні електричні заряди (електрони, іони), які будуть переміщуватись: позитивні – в напрямку поля, негативні – проти напрямку поля (рис. 7.2, а ). При цьому на одному кінці провідника буде накопичуватись надлишок позитивного заряду, а на іншому – негативного. Ці заряди називаються індукованими.

Переміщення зарядів відбуватиметься доти, доки Е всередині провідника не буде дорівнювати нулю (Е = 0), а лінії вектора напруженості електричного поля іззовні провідника – перпендикулярними до його поверхні (рис. рис. 7.2, б). З цього можна зробити такий висновок: незаряджений провідник, внесений в електростатичне поле, розриває певну частину ліній Е: ці лінії закінчуються на негативних індукованих зарядах і заново починаються на позитивних. При цьому індуковані заряди розподіляються на зовнішній поверхні провідника. Явище перерозподілу поверхневих зарядів на провіднику в зовнішньому електростатичному полі називається електростатичною індукцією.

Зазначимо, що, як це витікає з рис. 7.2, б, індуковані заряди з'являються на провіднику внаслідок зміщення їх під дією поля (тобто 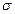є поверхневою густиною зміщених зарядів), причому, як було показано вище, електричне зміщення 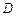поблизу провідника чисельно дорівнює поверхневій густині зміщених зарядів. Саме тому вектор 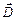отримав назву вектор електричного зміщення.

Слід звернути увагу на використання на практиці властивості зарядів розміщуватися на зовнішній стороні провідника. Так, всередині провідника роблять порожнину (адже в середині провідника завжди Е = 0 і тому створення всередині порожнини не вплине на розподіл зарядів в провіднику). Причому, у випадку заземлення такого провідника з порожниною потенціал у всіх точках порожнини буде нульовим: порожнина буде повністю ізольованою від впливу зовнішніх електростатичних полів. Це так званий електростатичний захист: коли, наприклад, електровимірювальний чи інший прилад хочуть захистити від впливу зовнішніх полів, його оточують провідним футляром (екраном). Такий екран можна зробити не суцільним, а у вигляді густої металевої сітки.

Електрична ємність відокремленого (самотнього) провідника

Відокремлений провідник – це провідник, який віддалений від інших провідників, тіл та зарядів.

Потенціал такого провідника прямо пропорційний його заряду і, як показують досліди, різні провідники, будучи однаково зарядженими, мають різні потенціали. Тому для самотнього провідника можна записати таку залежність:

.

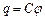Величину

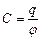
називають електроємністю (або просто ємністю ) самотнього провідника. Ємність самотнього провідника чисельно дорівнює заряду, надання якого провіднику змінює його потенціал на одиницю.

Ємність провідника залежить від його розмірів і форми і не залежить від матеріалу, форми і розміру порожнини всередині провідника; вона не залежить також від заряду провідника і від його потенціалу.

Одиниця ємності – фарад (Ф).1 Ф - це ємність такого самотнього провідника, потенціал якого змінюється на 1 В у разі надання йому заряду 1 Кл.

Розрахуємо ємність самотньої кулі радіуса 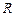, яка міститься в середовищі з діелектричною проникністю 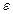. Оскільки потенціал такої кулі визначається залежністю

,

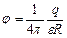то скориставшись формулою для ємності 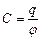і підставивши в неї вищенаведену залежність для 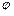, отримаємо таку формулу для ємності кулі:

.

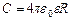З цієї формули витікає, що ємність 1 Ф має куля радіусом 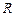= 9·10⁶км, що приблизно в 1400 раз більше радіуса Землі. Ємність Землі приблизно становить 0,7 мФ.

Таким чином, фарад – дуже велика величина, і тому на практиці використовують часткові (дольні) одиниці, а саме: міліфарад (мФ), мікрофарад (ммФ), нанофарад (нФ), пікофарад (пФ).

З формули для ємності кулі випливає, що одиниця електричної сталої 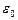– фарад на метр (Ф/м).

Конденсатори, їх типи та ємність

Самотні провідники мають дуже малу ємність (навіть куля таких розмірів як Земля має ємність лише 0,7 мФ). В той же час на практиці виникає потреба в пристроях, які могли б, маючи невеликі розміри, при невеликому відносно оточуючих тіл потенціалі накопичувати на собі (так би мовити "конденсувати") значні за величиною заряди, тобто мати велику ємність. Такі пристрої називають конденсаторами.

Конденсатори будуються на тому принципі, що ємність провідника зростає у разі наближення до нього інших тіл – внаслідок виникнення на провіднику зарядів, індукованих іншими тілами. Саме тому на практиці застосовуються конденсатори – системи з провідників, розміщених близько один відносно одного. Конденсатором називають систему з двох металевих електродів (обкладинок) з однаковими по модулю, але протилежними по знаку зарядами розміщених на близькій відстані один від одного і розділених шаром діелектрика. Щоб електричне поле в конденсаторах не змінювалось (або точніше майже не змінювалось) під дією зовнішніх полів це поле намагаються зосередити просторі між обкладинками. Цій вимозі задовольняють дві пластини, розміщені близько одна від одної, два коаксіальних циліндра і дві коаксіальні сфери. Відповідно до цього залежно від форми обкладинок конденсатори поділяють на плоскі, циліндричні та сферичні. За природою діелектрика між обкладинками конденсатора їх поділяють на повітряні, паперові, слюдяні, керамічні та електролітичні.

Ємність конденсаторів визначають за формулою:

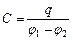
де 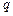– заряд однієї з обкладинок конденсатора; 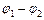– різниця потенціалів (або напруга) між ними.

Електричну ємність конденсатора вимірюють у тих самих одиницях, що і ємність самотнього провідника.

Розрахуємо ємність плоского, циліндричного та сферичного конденсаторів.

1) Ємність плоского конденсатора. Плоский конденсатор складається з двох паралельних металевих пластин площею 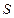кожна, які розташовані на відстані 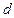одна від одної і мають заряди +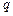і –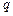(рис 7.3). Відстань 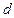між пластинами будемо вважати малою порівняно з лінійними розмірами цих пластин. Тому крайовими ефектами можна знехтувати і поле між обкладинками вважати однорідним. Це поле неважко розрахувати, скориставшись формулою для поля двох нескінченних паралельних різнойменно заряджених площин. Різниця потенціалів між такими площинами з поверхневою густиною заряду 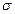, розташованими одна від одної на відстані 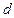, дорівнює:

.

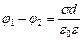Отже, підставивши в загальну формулу для обчислення ємності 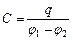величину 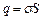, отримаємо таку формулу для ємності плоского конденсатора:

.

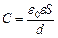2) Ємність циліндричного конденсатора. Для визначення ємності циліндричного конденсатора, який складається з двох порожнистих коаксіальних циліндрів з радіусами 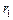і 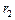(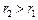), вставлених один в другий (рис. 7.4), знову таки знехтуємо крайовими ефектами і вважатимемо поле радіально-симетричним і зосередженим між циліндричними обкладинками. Різницю потенціалів між обкладинками розрахуємо за формулою для поля рівномірно зарядженого нескінченного циліндра з лінійною густиною 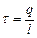(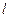– довжина обкладинок). У разі наявності діелектрика між обкладинками різниця потенціалів

.

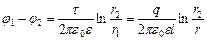Отже, підставивши цю формулу в формулу для ємності 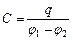, отримаємо такий вираз для ємності циліндричного конденсатора:

.

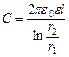3) Ємність сферичного конденсатора. Такий конденсатор складається з двох концентричних обкладинок, розділених сферичним шаром діелектрика (рис. 7.5). Оскільки різниця потенціалів між двома точками, що лежать на відстан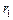і і 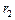(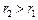) від центра зарядженої сферичної поверхні за наявності діелектрика між обкладинками визначається залежністю:

,

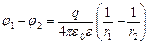то підставивши цю залежність в формулу для ємності 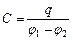, отримаємо такий вираз для ємності сферичного конденсатора:

.

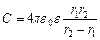У випадку малої величини зазора порівняно з радіусом сфери (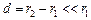) 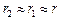вирази для ємності сферичного і плоского конденсаторів співпадають (оскільки 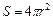– площа сферичної обкладинки):

.

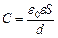
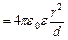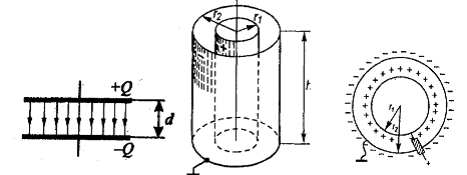
Рис. 7. 3 Рис. 7.4 Рис. 7.5

Лекція 08

Постійний електричний струм

Дата добавления: 2014-01-03