Закон Ома

Німецький фізик Г.Ом експериментально встановив закон, який носить його ім'я. Для однорідної ланки металевого провідника, тобто для такого провідника, який не містить джерела струму, закон Ома формулюється так:

Сила струму в провіднику прямо пропорційна прикладеній напрузі і обернено пропорційна опору провідника:

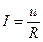
або в диференціальній формі (з урахуванням того, що 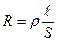; 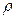– питомий електричний опір, 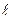і 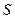– довжина провідника і його поперечний переріз):

,

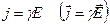де 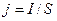– густина струму; 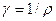– питома провідність.

Закон Ома для замкненої мережі (див. рис. 8.1) має таке формулювання: Сила струму в замкненій мережі дорівнює відношенню е.р.с. джерела струму до сумарного опору всієї мережі:

,

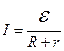де 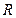– опір зовнішньої мережі; 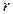– внутрішній опір джерела струму.

Напруга на зовнішній мережі:

.

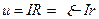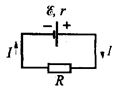
Рис. 8.1

Опір і провідність провідників

Визначення опору: Опір – це величина, яка характеризує опір провідника електричного струму.

Одиниця опору – Ом; 1 Ом – опір такого провідника, в якому при напрузі 1 В протікає постійний струм 1 А.

Електрична провідність 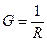. Одиниця електричної провідності – См; 1 См (сіменс) – провідність ланки електричної мережі опором 1 Ом.

Питома провідність (позначається: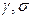): 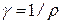. Одиниця провідності См/м.

Залежність 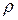і 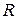від температури:

;

,

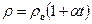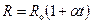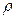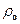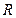де і , і 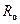– відповідно питомий опір і опір провідника при температурі 0 ºС; 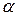– температурний коефіцієнт опору, який для чистих металів наближується до 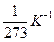. Отж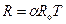е , де 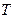- термодинамічна температура.

Якісний характер залежності 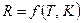для металів показано на рис. 8.2 (крива 1). Пізніше було виявлено, що опір багатьох металів, таких як 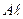, , 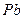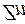та ін. і їх сплавів при дуже низьких температурах, названих критичними температурами для кожної речовини, скачкоподібно змінюються до нуля (крива 2), тобто метал стає абсолютним провідником.

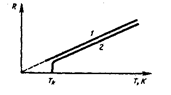
Рис.8.2

Надпровідність – це властивість металів та їх сплавів у випадку охолодження нижче критичної температури 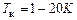(характерної для даного провідника) скачкоподібно змінювати свій опір до нуля.

Явище надпровідності для ртуті вперше в 1911 р. відкрив Г.Камерлінг-Оннес.

Робота та потужність електричного струму

Для визначення роботи і потужності електричного струму розглянемо однорідний провідник опором 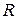, до кінців якого прикладено напругу 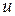. Тоді за час 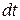через переріз провідника переноситься заряд 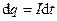, і робота струму буде такою:

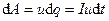, або

.

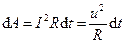Робота виражається в Дж.

Потужність струму (виражається в Вт):

.

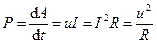Закон Джоуля–Ленца

Якщо струм проходить по нерухомому металевому провіднику, то вся робота струму витрачається на його нагрівання і, за законом збереження енергії

.

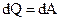Використовуючи вираз для роботи струму, одержуємо закон Джоуля–Ленца:

Закон Джоуля–Ленца в диференціальній формі. Виділимо в провіднику елементарний циліндровий об'єм dV = dSdt (вісь циліндра співпадає з напрямом струму), опір якого 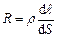. За законом Джоуля–Ленца, за час d t в цьому об'ємі виділиться теплота

.

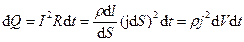Кількість теплоти, що виділяється за одиницю часу в одиниці об'єму, називається питомою тепловою потужністю струму:

.

.

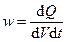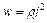Використовуючи диференціальну форму закону Ома (j = 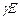) і співвідношення 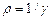, отримаємо:

.

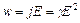Дві останні формули – закон Джоуля–Ленца в диференціальній формі.

Правила Кірхгофа для розгалужених кіл

Вузол електричного кола – це будь-яка точка розгалуження кола, в якій сходиться не менше трьох провідників із струмом (див. рис. 8.3). Струм, що входить у вузол, вважається позитивним (струми І ₁, І ₃), а струм, що виходить з вузла, – негативним (струми І ₂, І ₄, І ₅).

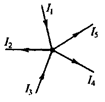
Рис. 8.3

Перше правило Кірхгофа. Алгебраїчна сума струмів, що сходяться у вузлі, дорівнює нулю: .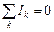

Друге правило Кірхгофа. В будь-якому замкненому контурі, довільно вибраному в розгалуженому електричному колі, алгебраїчна сума добутків сил струмів І_і на опір R_і відповідних ділянок цього контуру дорівнює алгебраїчній сумі е. р. с. €_к, що зустрічаються в цьому контурі:

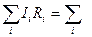
€_к

Під час розрахунку складних кіл із застосуванням правил Кірхгофа необхідно:

1. Вибрати довільний напрям струмів на всіх ділянках кола; дійсний напрям струмів визначається під час рішенні задачі: якщо шуканий струм вийде позитивним, то його напрям був вибраний правильно, негативним – його істинний напрям протилежно вибраному.

2. Вибрати напрям обходу контура і строго його дотримуватись; добуток IR позитивний, якщо струм на даній ділянці співпадає з напрямом обходу, і навпаки, е. р. с., які діють по вибраному напряму обходу, вважаються позитивними, проти – негативними.

3. Скласти таку кількість рівнянь, щоб їх число дорівнювало числу розшуканих величин (в систему рівнянь повинні входити всі опори і е. р. с. даного кола); кожний даний контур повинен містити хоча б один елемент, який відсутній в попередніх контурах, інакше вийдуть рівняння, що є простою комбінацією вже складених.

Лекція 09.

Магнітне поле постійного струму

Загальний опис магнітного поля

Магнітне поле – це силове поле в просторі, що оточує електричні струми і постійні магніти.

Магнітне пoлe створюється лише зарядами, що рухаються, і діє тільки на електричні заряди, що рухаються в цьому полі. Характер впливу магнітного поля на струм різний – залежно від форми провідника, по якому тече струм, його розташування, напрямку струму. Тому для характеристики магнітного поля треба розглянути його дію на певний струм.

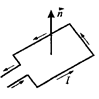
Під час дослідження магнітного поля використовується замкнений плоский контур зі струмом (рамка зі струмом), розміри якого малі порівнянні з відстанню до струмів, що утворять магнітне поле. Орієнтація контуру в просторі характеризується напрямком нормалі до нього, причому за позитивний напрямок нормалі приймається напрямок, який пов'язаний зі струмом правилом правого гвинта, тобто за позитивний напрямок нормалі приймається напрямок поступального руху гвинта, голівка якого обертається, у напрямку струму, що тече в рамці (рис. 9.1).

Вибір напрямку магнітного поля. За напрямок магнітного поля в даній точці приймається напрямок, уздовж якого розташовується позитивна нормаль до вільно підвішеної рамки зі струмом (рис. 9.2) або напрямок, що збігається з напрямком сили, яка діє на північний полюс магнітної стрілки, поміщеної в дану точку. Оскільки обидва полюса магнітної стрілки лежать у близьких точках поля, то сили, що діють на обидва полюси, однакові. Отже, на магнітну стрілку діє пара сил, яка повертає її так, щоб вісь стрілки, що з'єднує південний полюс з північним, збігалася з напрямком поля.

_

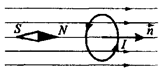
Рис. 9.1 Рис. 9.2

2. Потік вектора магнітної індукції. Теорема Остроградського-Гаусса для поля В

Потік вектора магнітної індукції (магнітний потік) крізь площадку dS – це скалярна фізична величина

,

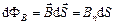де 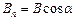– проекція вектора 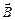на напрям нормалі до площадки d S (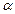– кут між векторами 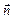і 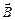), 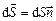– вектор, модуль якого дорівнює d S, а напрям співпадає з напрямом 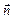до площадки.

Знак потоку залежить від cos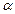. Потік вектора 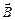пов'язують з контуром, по якому тече струм. А тоді позитивний напрям нормалі визначено (він зв'язується із струмом правилом правого гвинта). Магнітний потік, створюваний контуром через поверхню, обмежену ним самим, завжди позитивний.

Магнітний потік крізь довільну поверхню S

.

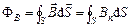Якщо поле однорідне, поверхня плоска і перпендикулярна вектору В, то тоді

Ф _В = BS.

Одиниця – Вб. 1 Вб (вебер) – це магнітний потік, що проходить через плоску поверхню площею 1 м², розташовану перпендикулярно однорідному магнітному полю, індукція якого дорівнює 1 Тл.

Теорема Остроградського-Гаусса для поля В. Потік вектора магнітної індукції крізь довільну замкнену поверхню дорівнює нулю:

.

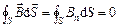Ця теорема відображає факт відсутності магнітних зарядів, наслідком чого є той факт, що лінії магнітної індукції не мають ні початку, ні кінця і є замкненими.

3. Закон Біо-Савара-Лапласа та приклади його застосування (визначення індукції магнітного поля прямолінійного провідника зі струмом і магнітне поле в центрі кругового струму)

Магнітне поле постійних струмів вивчалось французькими вченими Ж. Біо і Ф. Саваром і результати проведених дослідів були узагальнені П.Лапласом.

Для провідника з струмом 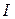, елемент 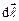якого створює в довільній точці А (рис. 9.3) індукцію 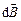, матимемо:

,

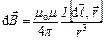де 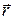– радіус-вектор, проведений з елемента 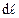провідника в точку А.

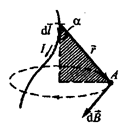
Рис. 9.3

Зазначимо, що 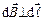і 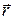і направлений вздовж дотичної до лінії магнітної індукції. Напрям 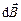визначають по правилу правого гвинта: напрям обертання головки гвинта дає напрям 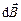, якщо поступальний рух гвинта відповідає напряму струму в елементі

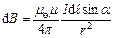, (1)

де 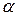– кут між векторами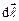і .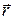

Розглянемо 2 приклади застосування цього закону.

1. Магнітне поле прямолінійного провідника зі струмом (рис. 9.4). Такий струм створюється нескінченно довгим тонким провідником.

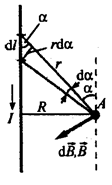
Рис. 9.4

Оскільки для такого провідника, як видно з рис. 9.4

, ,

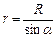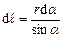то підставивши ці залежності в формулу (1), отримаємо

.

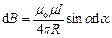Кут 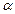для всіх елементів прямого проводу змінюється від 0 до 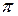. Тоді

.

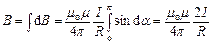2. Контур зі струмом в магнітному полі. Магнітний момент струму. Обчислимо магнітну індукцію кругового витка зі струмом на відстані 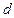від його центра (рис. 9.5).

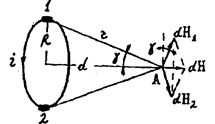
Рис. 9.5

Кожний елемент струму, наприклад елемент 1, створює у точці А магнітну індукцію поля 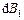. Індукція двох елементів, розташованих один напроти одного (1 і 2), додається і утворює магнітну індукцію 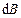, направлену уздовж осі, і отже, саме туди направлена і результуюча індукція В. Проекція 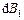, на напрямок В визначається як

=

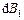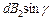
Оскільки 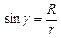, то, скорис­тавшись (1), при 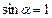матимемо

=

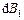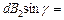
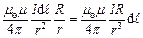
Загальна магнітна індукція

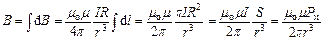, (2)

де 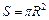– площа, що охоплюється струмом; 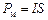– магнітний момент струму (за аналогією з електричним моментом диполя. У векторному запису 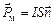, де 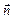– одиничний вектор, направлений уздовж нормалі до .

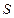З формули для В видно, що магнітна індукція кругового струму зменшується з відстанню пропорційно до 2³, як і напруженість електричного поля диполя.

3. Магнітна індукція в центрі кругового контуру зі струмом (рис. 9.6) може бути отримана і безпосередньо. Як видно з рисунка, всі елементи такого провідника створюють в центрі магнітні поля одного і того ж самого напрямку – вздовж нормалі до витка. Тому (як і в попередньому прикладі) додавання векторів 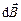можна замінити додаванням їх модулів.

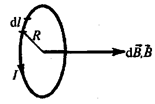
Рис.

Оскільки всі елементи провідника перпендикулярні 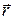(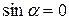) і відстань всіх елементів провідника до центра кругового струму однакова і дорівнює 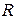, то

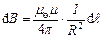
і, отже,

.

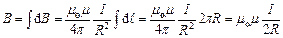Цей самий результат можна безпосередньо отримати і з загальної формули (2).

4. Теорема про циркуляцію векторів магнітної індукції та напруженості

магнітного поля

Циркуляція вектора 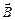вводиться аналогічно циркуляції вектора напруженості електростатичного поля.

Циркуляцією вектора 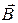по замкненому контуру називається інтеграл

,

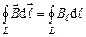де 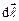– елемент довжини контуру, направлений вздовж обходу контуру, 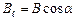– складова вектора 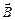в напрямку дотичної до контуру (з врахуванням вибраного напрямку обходу); 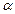– кут між векторами 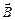і .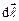

Теорема про циркуляцію вектора 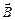(або закон повного струму) для магнітного поля в вакуумі формулюється так: циркуляція вектора 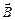по довільному контуру дорівнює добутку вектора магнітної сталої 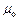на алгебраїчну суму струмів, які охоплюються цим контуром:

,

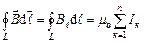де 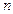– число провідників зі струмом, які охоплюються контуром 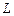довільної форми.

Зауваження до цієї теореми:

1) Теорема справедлива лише для магнітного поля в вакуумі (оскільки для поля в речовині необхідно враховувати молекулярні струми.

2) Кожен струм враховується стільки разів, скільки раз він охоплюється контуром; при цьому струм вважається додатнім (позитивним), якщо напрям його протікання пов'язано з напрямом обходу контура правилом правого гвинта, струм протилежного напряму вважається від'ємним (негативним).

3) Оскільки циркуляція вектора 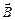магнітного поля не дорівнює нулю, то таке поле називається вихровим полем (на відміну від циркуляції вектора електростатичного поля, яка дорівнює нулю, а тому електростатичне поле є полем потенціальним.

Аналогічний вид має теорема про циркуляцію вектора 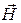для магнітного поля

.

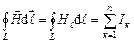ЛЕКЦІЯ 10

Дія магнітного поля на рухомі заряди

1. Магнітне поле рухомого заряду

Кожен провідник зі струмом створює в оточуючому просторі магнітне поле. Електричний струм – це упорядкований рух електричних зарядів, і тому можна вважати, що будь-який заряд, що рухається в вакуумі чи середовищі, створює навколо себе магнітне поле.

В результаті узагальнення дослідних даних був встановлений наступний закон, який визначає поле 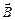точкового заряду 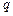, який вільно рухається з нерелятивістською швидкістю 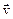(тобто з постійною швидкістю),

, ,

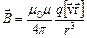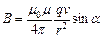де 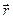– радіус-вектор, проведений від заряду 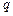до точки спостереження М (рис. 10.1); 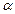– кут між 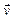і .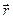

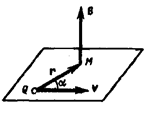
Рис. 10.1

2. Дія магнітного поля на рухомий заряд. Сила Лоренца

Сила, яка діє на електричний заряд, що рухається в магнітному полі з швидкістю 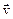, називається силою Лоренца і виражається формулою:

, ,

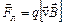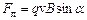де 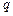– електричний заряд, що рухається із швидкістю 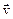в магнітному полі з індукцією 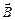, 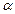– кут між 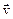і .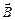

Зазначимо, що магнітне поле не діє на електричний заряд, що покоїться. В цьому полягає істотна відмінність магнітного поля від електричного. Магнітне поле діє тільки на заряди, що рухаються в ньому.

Напрям сили Лоренца визначається за допомогою правила лівої руки: якщо долоню лівої руки розташувати так, щоб в неї входив вектор 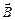, а чотири витягнуті пальці направити уздовж вектора 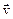(для 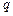> 0 напрями І і 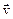співпадають, для 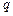< 0 – протилежні), то відігнутий великий палець покаже напрям сили, що діє на позитивний заряд (див. рис. 10.2).

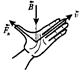
Рис. 10.2

Сила Лоренца перпендикулярна векторам 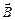і 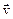. На рис. 10.3 показані напрями сил, з якими магнітне поле діє на заряджені рухомі частинки. Сила Лоренца не здійснює роботи.

Магнітне поле не діє на електричний заряд, що покоїться. Циммагнітне поле істотно відрізняється від електричного. Магнітне поле діє тільки на що рухаються в ньому заряди.

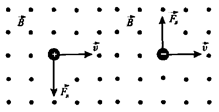
Рис. 10. 3

Формула Лоренца визначає силу у випадку, коли на заряд, що рухається, одночасно діють магнітне поле з індукцією 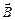і електричне поле з напруженістю :

.

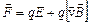3. Рух зарядженої частинки в магнітному полі

Вважаємо, що магнітне поле однорідне і на частинку не діють електричні поля.

1. Заряджена частинка рухається в магнітному полі із швидкістю 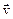уздовж ліній магнітної індукції (кут а між векторами 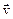і 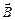дорівнює 0 або 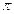). Тоді сила Лоренца рівна нулю, тобто магнітне поле на частинку не діє і вона рухається рівномірно і прямолінійно.

2. Заряджена частинка рухається в магнітному полі із швидкістю 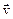, перпендикулярною вектору 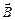( кут 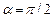). Тоді 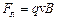: постійна по модулю і нормальна до траєкторії частинки. Частинка рухатиметься по колу, радіус 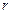якого визначається з умови

,

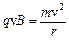звідки

.

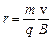Період обертання частинки, тобто час Т, протягом якого вона здійснює один повний оборот, дорівнює

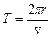
Підставивши сюди вираз для 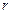, отримаємо

.

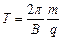3. Заряджена частинка рухається із швидкістю 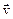під кутом 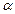до вектора 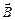(рис. 10. 4).

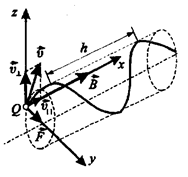
Рис. 10. 4

Рух частинки можна представити у вигляді суперпозиції:

1) рівномірного прямолінійного руху уздовж поля з швидкістю ;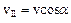

2) рівномірного руху із швидкістю 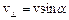по колу в площині, перпендикулярній полю. В результаті складання обох рухів виникає рух по спіралі, вісь якої паралельна магнітному полю. Крокгвинтової лінії

,

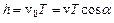де Т= 2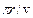– період обертання частинки. Підставивши відповідні вирази, отримаємо

.

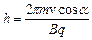Дата добавления: 2014-01-03