Метод контурных токов в матричной форме. Обучение стимулирует, ведет за собой развитие, в то же время опирается на него, но не надстраивается чисто механически

Обучение стимулирует, ведет за собой развитие, в то же время опирается на него, но не надстраивается чисто механически.

Вне обучения не может быть полноценного развития личности.

Современная отечественная педагогика стоит на точке зрения диалектической взаимосвязи обучения и развития личности, отводя, согласно положению Л.С. Выготского, ведущую роль обучению.

Обучение и развитие тесно связаны друг с другом: развитие и обучение не два параллельно протекающих процесса, они находятся в единстве.

Список литературы:

1. Бордовская Н., Реан А. Педагогика. Учебное пособие. – СПб.: Питер, 2011.

2. Вульфов Б.З., Иванов В.Д., Пидкасистый П.И. Педагогика. Учебное пособие под ред. П.И. Пидкасистого. – СПб.: Юрайт-Издат, 2011.

3. Ефремов О.Ю. Педагогика. Учебное пособие. – СПб.: Питер, 2010.

4. Коджаспирова Г.М. Педагогика. – Москва, Кнорус, 2011.

5. Педагогика: Учебник / под ред. Л.П. Крившенко. - М.: Проспект, 2009.

6. Сластенин В.А. и др. Педагогика: Учеб. пособие для студ. высш. пед. учеб. заведений. - М.: Академия, 2002.

В соответствии с введенным ранее понятием матрицы главныхконтуров В, записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.

Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c=n-m+1. Выражение (6) запишем следующим образом:

.

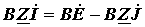(7)

В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения

,

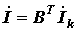(8)

где 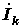- столбцовая матрица контурных токов; 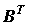- транспонированная контурная матрица.

С учетом (8) соотношение (7) можно записать, как:

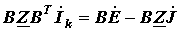
(9)

Полученное уравнение представляет собойконтурные уравнения в матричной форме. Если обозначить

,

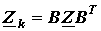(10)

.

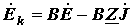(11)

то получим матричную форму записи уравнений, составленных по методу контурных токов:

,

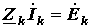(12)

где 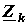- матрица контурных сопротивлений; 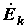- матрица контурных ЭДС.

В развернутой форме (12) можно записать, как:

,

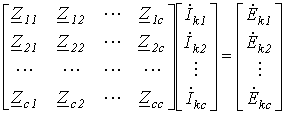(13)

то есть получили известный из метода контурных токов результат.

Рассмотрим пример составления контурных уравнений.

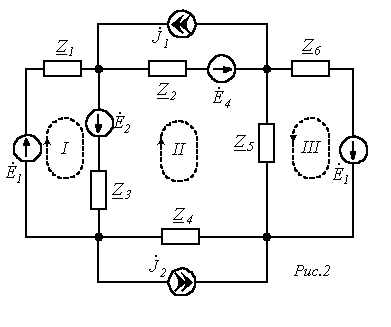
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла (m=4) и шесть обобщенных ветвей (n=6). Число независимых контуров, равное числу ветвей связи,

c=n-m+1=6-4+1=3.

Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.

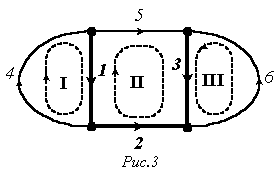Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:

В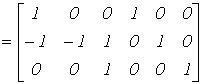

.Диагональная матрица сопротивлений ветвей

Z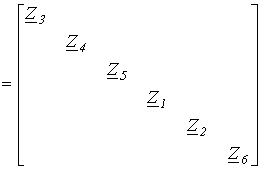

Матрица контурных сопротивлений

Zk = B Z B^T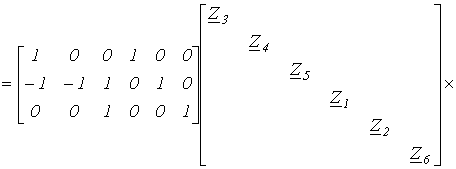

.

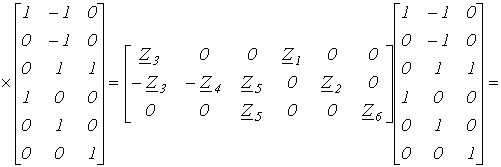
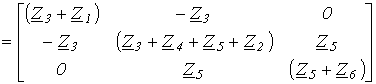Матрицы ЭДС и токов источников

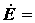
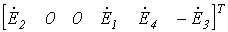
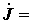
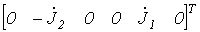
Тогда матрица контурных ЭДС

.

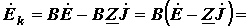
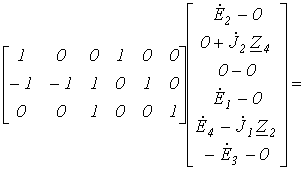
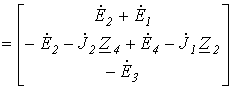Матрица контурных токов

.

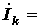
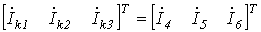Таким образом, окончательно получаем:

,

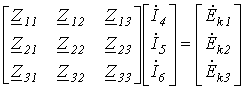где ; ; ; ; ; ; ; ; .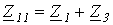

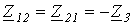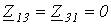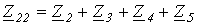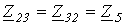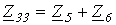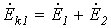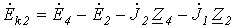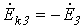Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.

Дата добавления: 2014-01-03