
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Буквы) и квалитета (цифры). Например: H7, a7, c8, c6, c12, C7, R6, d8
|
|
|
|
Поле допуска размера образуется сочетанием основного отклонения
Начертите cхемы полей допусков, указанных в примере, подберите числовые значения предельных отклонений для указанных полей допусков, пользуясь таблицей основных отклонений (прилож.1).
Пример определения числовых значений предельных отклонений 5
полей допусков для Ø10, заданных в условном (буквенном)
обозначении: 1) Ø10с6, 2) Ø10с8, 3) Ø10с12
и построения схем заданных полей допусков
1. Определить числовое значение основного отклонения – с:
заданные обозначения полей допусков относятся к валу, т.к. основное отклонение
– «с» обозначено строчной буквой; по таблицам основных отклонений для валов,
для номинального размера 10 определяем числовое значение основного отклонения
с = –80мкм или = – 0,080мм, (прилож.3); это предельное отклонение, согласно
определению, является ближайшим к нулевой линии, тогда второе предельное отклонение будет находиться еще дальше от нулевой линии;
так как все три поля допуска имеют основное отклонение – с, то схематично все три поля допуска начинаются на одном уровне от нулевой линии:
|


 0±
0±










1. Второе предельное отклонение располагается от нулевой линии на расстоянии, состоящим из числового значения основного отклонения и допуска, определяемого квалитетом; основные отклонения со знаком – «минус» всегда являются верхними ( es), следовательно, второе предельное отклонение относительно основного будет нижним (ei);
согласно таблице допусков (стр.3) определяем величину допуска для номинального размера 10 и заданного квалитета для всех трех вариантов:
1) IT6 (допуск 6 -го квалитета) – 9мкм или 0,009мм; 2) IT8 (допуск 8 -го квалитета) – 22мкм или 0,022мм; 3) IT10 (допуск 10 -го квалитета) – 150мкм или 0,150мм
Согласно выражению: Тd = es – ei (cтр.1), получаем: ei = es – T,
в результате нижнее предельное отклонение ( ei ) равно:
1) ei = – 0,080 – 0,009= – 0,089; 2) ei= – 0,080 – 0,022 = – 0,102
3) ei = – 0,080 – 0,150 = – 0,230
таким образом, числовое выражение полей допусков (в виде двух предельных
отклонений) и схемы полей допусков согласно рассчитанным предельным
отклонениям выглядят следующим образом:
|
|
| ||||||
Ø10с6 (); Ø10с8 (); Ø10с12 ()

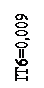
|

 0±
0±








|






|


 |
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 211; Нарушение авторских прав?; Мы поможем в написании вашей работы!