Деление чисел со знаком

Деление чисел без знака

Для деления чисел без знака предназначена команда

div делитель

Делитель может находиться в памяти или в регистре и иметь размер 8, 16 или 32 бит. Местонахождение делимого фиксировано и так же, как в команде умножения, зависит от размера операндов. Результатом команды деления являются значения частного и остатка.

Варианты местоположения и размеров операндов операции деления показаны в таблице 11.

Таблица 11. Расположение операндов и результата при делении

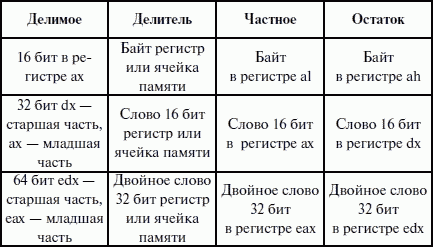
После выполнения команды деления содержимое флагов неопределенно, но возможно возникновение прерывания с номером 0, называемого «деление на нуль». Этот вид прерывания относится к так называемым исключениям. Эта разновидность прерываний возникает внутри микропроцессора из-за некоторых аномалий во время вычислительного процесса. Прерывание О, «деление на нуль», при выполнении команды div может возникнуть по одной из следующих причин:

1) делитель равен нулю;

2) частное не входит в отведенную под него разрядную сетку, что может произойти в следующих случаях:

а) при делении делимого величиной в слово на делитель величиной в байт, причем значение делимого в более чем 256 раз больше значения делителя;

б) при делении делимого величиной в двойное слово на делитель величиной в слово, причем значение делимого в более чем 65 536 раз больше значения делителя;

в) при делении делимого величиной в учетверенное слово на делитель величиной в двойное слово, причем значение делимого в более чем 4 294 967 296 раз больше значения делителя.

Для деления чисел со знаком предназначена команда

idiv делитель

Для этой команды справедливы все рассмотренные положения, касающиеся команд и чисел со знаком. Отметим лишь особенности возникновения исключения 0, «деление на нуль», в случае чисел со знаком. Оно возникает при выполнении команды idiv по одной из следующих причин:

1) делитель равен нулю;

2) частное не входит в отведенную для него разрядную сетку.

Последнее в свою очередь может произойти:

1) при делении делимого величиной в слово со знаком на делитель величиной в байт со знаком, причем значение делимого в более чем 128 раз больше значения делителя (таким образом, частное не должно находиться вне диапазона от —128 до + 127);

2) при делении делимого величиной в двойное слово со знаком на делитель величиной в слово со знаком, причем значение делимого в более чем 32 768 раз больше значения делителя (таким образом, частное не должно находиться вне диапазона от —32 768 до +32 768);

3) при делении делимого величиной в учетверенное слово со знаком на делитель величиной в двойное слово со знаком, причем значение делимого в более чем 2 147 483 648 раз больше значения делителя (таким образом, частное не должно находиться вне диапазона от —2 147 483 648 до [phone]).

Дата добавления: 2017-01-14