ЛВП R3 и ЛВП направленных отрезков

Введение в философию. Учебник. Под. Ред. Фролова И.Т. М.,1989. Часть 2. Глава 6.

Понятия

Материя, атрибутивные свойства материи, система, структура, элемент, структурный уровень организации, движение, развитие, синергетика, самоорганизация, пространство, время, единство мира.

Литература

2. Барашенков В.С. Кварки, протоны, Вселенная. М., 1987.
3. Дубровский В.Н., Молчанов Ю.Б. Эволюционирует ли время, пространство и причинность?// Вопросы философии. 1986. №6.
4. Гегель Г. В. Ф. Сочинения. М., 1974. Т. 1, С. 150.

5. Гегель Г.В.Ф. Энциклопедия философских наук. М., 1974. Т. 1. С. 275.

6. Герцен А.И. Письма об изучении природы. М., 1946. С. 105—106.

7. Кант И. Сочинения. М., 1965. Т. 3. С. 521.

8. Кузнецов Б.Г. Современная наука и философия. М., 1981.

9. Ленин В.И. Материализм и эмпириокритицизм. ПСС. Т.18.
10. Миронов В.В. Философия. М., 2004

11. Моисеева Н.А. Сороковикова В.И. Философия. К., 20085. Моисеев Н.Н. Мир XXI века и христианская традиция // Вопросы философии. 1993. №8.

В средней школе было введено понятие «геометрического вектора» – направленного отрезка длиной . Во множестве L={ } были определены:

- равенство ⊜: Н.О. ;

- сложение ⊕: правило параллелограмма и

2

с=a - b

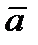
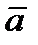
d=a+b

- умножение на вещественное число с⊙

Проверьте, что множество L={ } является Линейным Векторным Пространством.

Например, ∃! нулевой Н.О. ∃! П ротивоположный Н.О.

Z

Y

B(x_B,y_B,z_B)

A(x_A,y_A,z_A)  

O

X

В прямоугольной системе координат XYZ «геометрический вектор – направленный отрезок» задаётся своими координатами - алгебраическими проекциями Н.О. на координатные оси:

OA (x_A,y_A,z_A), OB (x_B,y_B,z_B),

---------------------------------------------------------------------------------------------------------------------------------------

В дальнейшем будем отождествлять ЛВП R³ и ЛВП Н.О. в координатном пространстве:
- «изображать» вектор в виде направленного отрезка и
- использовать для решения «геометрических задач» аппарат векторной алгебры.

С О О Т В Е Т С Т В И Е П О Н Я Т И Й

ЛВП R³ ↔ ЛВП Н.О.

Стандартный базис

(1)-вектор ↔ {x,y,z} – направленный отрезок,

(2)- норма вектора 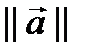= длина Н.О.,

(3) - коллинеарность векторов ↔ параллельность Н.О.:
(координаты коллинеарных векторов пропорциональны)

Дата добавления: 2017-01-14