На 2013/14 учебный год

Контрольная работа по аналитической геометрии в пространстве

Mark the suitable word or phrase.

Match the questions in activity 16. With these answers.

Complete the questions with one word.

Put the words in the correct order.

1.Is a she women kind very. 3.Are the colleges beautiful.

2.City a big London is very. 4.Very he teacher friendly is a.

1. … is his job?

2. … are they from?

3. … many students are there in the class?

4. … old are you?

5. … colour is your coat?

6. … is your book?

1.Blue 2.Twelve 3.Waiter 4.Twenty-one 5.Brazil 6.On the table.

His

1.Dieter is from Bonn. a journalist.

He’s

They’re

2.Christine and Julia are English. good friends.

There are

teacher

3.The are very kind.

teachers

has

4.He got a blue pen.

have

There

5. are two computers in each classroom.

Their

Are

6. you got a mobile phone?

Have

are

7.The people very friendly.

have

We

8. school is very modern.

Our

для студентов 1 ОЗО отделения математики

факультета математики, информатики и физики Южного федерального университета

Составитель: доц. И.А. Бреус.

Вариант 1

1. Векторы а и b образуют угол φ = . Зная, что | а | = 6, | b | = 5, вычислить

|[аb] |.

2. Даны три вектора:

a = {1; — 1; 3}, b = { — 2; 2; 1}, с = {3;—2;5}.

Вычислить a b c.

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) х = 0; 2) у = 0.

4. Составить уравнения линии пересечения плоскости Oxz и сферы с центром в начале координат и радиусом, равным 3.

5. Составить уравнение плоскости, которая проходит через точку M₁(2; 1; —1) и имеет нормальный вектор n ={1, —2; 3}.

6. Привести уравнение плоскости к нор­мальному виду:

2 х —2 у + 2 —18 = 0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

х + у + z —10 = 0.

8. Составить каноническое уравнение прямой, проходящей через точку М ₁ (2; 0; — 3) параллельно: вектору а = {2; —3; 5}.

9. Составить уравнение сферы в случае, если сфера имеет центр С(0; 0; 0) и радиус r =9.

10. Установить, что плоскость х — 2 = 0 пересекает эллип­соид

по эллипсу; найти его полуоси и вершины.

Вариант 2

1. Даны: |а| = 10, |b| = 2 и a b=12. Вычислить |[аb] |.

2. Установить, компланарны ли векторы а, b, с, если:

a = {2;3; — 1}, b = {l; - 1;3}, c = { 1; 9; — 11};

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) z = 0; 2) х —2 = 0.

4. Составить уравнения линии пересечения сферы, центр ко­торой находится в начале координат и радиус равен 5, с плоско­стью, параллельной плоскости Охz и лежащей в левом полупро­странстве на расстоянии двух единиц от нее.

5. Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор п = {5; 0; —3}.

6. Привести уравнение плоскости к нор­мальному виду:

х — у —z + 16 = 0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

х — у — z +16 = 0.

8. Составить каноническое уравнение прямой, проходящей через точку М ₁ (2; 0; — 3) параллельно прямой .

9. Составить уравнение сферы в случае, если сфера имеет центр С (5; — 3; 7) и радиус г = 2.

10. Установить, что плоскость z+ 1 = 0 пересекает однополостный гиперболоид

по гиперболе; найти её полуоси и вершины.

Вариант 3

1. Даны: |а| = 3, |b| = 26 и |[ab]| = 72. Вычислить аb.

2. Установить, компланарны ли векторы а, b, с, если:

a = {3; — 2; 1 }, b = {2;1;2}, с = {3; — 1; —2);

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) y + 2 = 0; 2) z + 5 = 0.

4. Составить уравнения линии пересечения плоскости Oyz и сферы, центр которой находится в точке С (5; —2; 1) и радиус равен 13.

5. Точка Р (2; —1; —1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравне­ние этой плоскости.

6. Привести уравнение плоскости к нор­мальному виду:

4 х — 6у — 12z — 11=0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

х + z —6 = 0.

8. Составить каноническое уравнение прямой, проходящей через точку М ₁ (2; 0; — 3) параллельно оси Ох.

9. Составить уравнение сферы в случае, если сфера проходит через начало координат и имеет центр С (4; -4; —2).

10. Установить, что плоскость _у + 6 = 0 пересекает гипер­болический параболоид

по параболе; найти ее параметр и вершину.

Вариант 4

1. Векторы а и b взаимно перпендикулярны. Зная, что |а|— = 3, |b|= 4, вычислить:

1) |[(a + b) (a- b)]|; 2) | [(3a—b)(a—2b)]|.

2. Установить, компланарны ли векторы а, b, с, если:

а = {2; —1; 2}, b = {1;2;— 3 }, с = {3;— 4; 7 }.

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) х³ + у² + z² = 25; 2) (х — 2)² + (у + 3)² + (z — 5)² = 49.

4. Составить уравнения линии пересечения двух сфер, одна из которых имеет радиус, равный 6, и центр в начале координат, дру­гая имеет радиус, равный 5, и центр С(1; —2; 2).

5. Даны две точки М₁(3; —1; 2) и М₂(4; —2; —1). Соста­вить уравнение плоскости, проходящей через точку М₁ перпендику­лярно к вектору .

6. Привести уравнение плоскости к нор­мальному виду:

— 4 x — 4 у + 2z + 1 =0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

у — z + 2 = 0.

8. Составить каноническое уравнение прямой, проходящей через точку М ₁ (2; 0; — 3) параллельно оси Оу.

9. Составить уравнение сферы в случае, если сфера проходит через точку А (2; — 1; — 3) и имеет центр С (3; —2; 1).

10. Установить, какая линия является сечением эллипсоида плоскостью

2х —Зу + 4z —11=0, и найти её центр.

Вариант 5

1. Векторы а и b образуют угол φ = 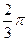. Зная, что |а| = 1, |b| = 2, вычислить:

1 ) [a b]²; 2) [(2а + b)(а + 2b)]²; 2) [(а + 3b)(3а — b)}²;

2. Доказать, что четыре точки

А(1; 2; —1), В (0; 1; 5), С (—1; 2; 1), D (2; 1; 3)

лежат в одной плоскости.

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) х² + 2у² + 3z² = 0; 2) х² + 2у² + 3z² + 5 = 0.

4. Найти точки пересечения трех поверхностей:

х² +y²+x^{2 =}49, у — 3 = 0, z + 6 = 0.

5. Составить уравнение плоскости, проходящей через точку M₁ (3;4; —5) параллельно двум векторам a₁ = {3; 1; —1} и a₂ = {1; —2; 1}.

6. Привести уравнение плоскости к нор­мальному виду:

5 у — 12 z + 26 = 0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

х + у + 10 = 0.

8. Составить каноническое уравнение прямой, проходящей через точку М ₁ (2; 0; — 3) параллельно оси Oz.

9. Составить уравнение сферы в случае, если точки А (2; — 3; 5) и В (4; 1; — 3) являются концами одного из диаметров сферы.

10. Установить, какая линия является сечением гиперболиче­ского параболоида плоскостью Зх—Зу + 4z + 2 = 0, и найти её центр.

Вариант 6

1. Даны векторы

а = {3; — 1; — 2} и b = {1;2;—1}.

Найти координаты векторных произведений:

1) [ab]; 2) [(2a + b)b]; 3) [(2a —b)(2a + b)].

2. Вычислить объём тетраэдра, вершины которого находятся в точках А (2; —1; 1), В (5; 5; 4), С (3; 2; — 1) и D (4; 1; 3).

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) х — у =0; 2) х + z = 0.

4. Найти точки пересечения трёх поверхностей:

х² +y²+x^{2 =}9, x²+y² +(z — 2)² = 5, y - 2 = 0.

5. Составить уравнение плоскости, проходящей через точки M ₁(2; — 1; 3) и М ₂(3; 1; 2) параллельно вектору а = {3; — 1; —4}.

6. Привести уравнение плоскости к нор­мальному виду:

3 х — 4 у — 1=0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

z— 2 = 0.

8. Составить каноническое уравнение прямой, проходящей через две данные точки:

(1; — 2; 1), (3; 1; —1).

9. Составить уравнение сферы в случае, если центром сферы является начало координат, и плоскость 16х — 15у — 12z + 75 = 0 является касательной к сфере.

10. Доказать, что эллиптический параболоид имеет одну общую точку с плоскостью 2 х — 2 у — z — 10 = 0, и найти её координаты.

Вариант 7

1. Даны точки А(2; — 1; 2), B(1;2; — 1) и C(3; 2; 1). Найти коор­динаты векторных произведений 1) [ ]; 2) [( — 2 ) ].

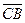2. Определить, какой является тройка а, b, с (правой или левой), если:

1) а = k, b = i, с = у; 2)а = i, b = k, c = j;

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) у — 2 = 0; 2) ху = 0.

4. Даны точки M ₁(3; 4; —4), M ₂(—3; 2; 4). Определить, какие из них лежат на линии

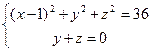
и какие не лежат на ней.

5. Составить уравнение плоскости, проходящей через три точки: М ₁ (3; — 1; 2), М ₂ (4; — 1; — 1) и М ₃ (2; 0; 2).

6. Привести уравнение плоскости к нор­мальному виду: у + 2 = 0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат: 2 х + 1 = 0.

8. Составить каноническое уравнение прямой, проходящей через две данные точки:

(3; —1; 0),(1; 0, —3).

9. Составить уравнение сферы в случае, если сфера имеет центр С (3; — 5; — 2), и плоскость 2х — у — Зz + 11 = 0 является касательной к сфере.

10. Доказать, что двуполостный гиперболоид имеет одну общую точку с плоскостью 5 х + 2 z + 5 = 0, и найти её координаты.

Вариант 8

1. Вычислить синус угла, образованного векторами а = {2; —2; 1} и b = {2; 3; 6}.

2. Определить, какой является тройка а, b, с (правой или левой), если:

1) a = j, b = i, c = k; 2) а = i + y, b = j, c = k;

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) хz = 0; 2) yz = 0.

4. Даны точки М₁(— 1— 4; 4) и M ₂(2; 3; —3). Определить, какие из них лежат на линии

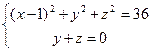
и какие не лежат на ней.

5. Установить, какие из следующих пар уравнений определяют параллельные плоскости:

1) 2х — 3у + 5z — 7 = 0, 2х — 3у + 5z + 3 = 0;

2) 4х+2у —4z + 5 = 0, 2х + у + 2z—1=0;

3) х—3z +2 = 0, 2х —6z — 7 = 0.

6. Привести уравнение плоскости к нор­мальному виду:

— х + 5 = 0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

2 у + 1=0.

8. Составить каноническое уравнение прямой, проходящей через две данные точки:

(0; —2; 3), (3; -2; 1).

9. Составить уравнение сферы в случае, если сфера проходит через три точки M ₁(3; 1; — 3), M ₂(— 2; 4; 1) и M ₃(— 5; 0; 0), аее центр лежит на плоскости 2х + у — 2 + 3 = 0.

10. Доказать, что эллипсоид имеет одну общую точку с плоскостью

4 х — 3 у + 12 z — 54 = 0, и найти её координаты.

Вариант 9

1. Вектор х, перпендикулярный к векторам а = { 4; — 2; — 3 } и a = {0; 1; 3}, образует с осью Оу тупой угол. Зная, что | х | = 26, найти его координаты.

2. Определить, какой является тройка а, b, с (правой или левой), если:

1) a = i + j, b = i — j, c= j; 2) a = i + y, b = i — j, c = k.

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) хуz = 0; 2) х² —4х = 0.

4. Определить, какие из следующих линий проходят через начало координат:

1) 2)

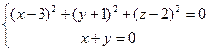
3)

5. Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости:

1) 3 х — у — 2 z — 5 = 0, х + 9 у — 32 + 2 = 0;

2) 2 х + 3 у —2 —3 = 0, х — у — z + 5 = 0;

3) 2 х —5у + z = 0, х + 22 —3 = 0.

6. Привести уравнение плоскости к нор­мальному виду:

— z + 3 = 0;

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

х — 2 у + 2 z — 6 = 0.

8. Составить каноническое уравнение прямой, проходящей через две данные точки:

(1; 2; —4), (—1; 2; —4).

9. Составить уравнение сферы в случае, если сфера проходит через четыре точки: M ₁(l; —2; — 1), М ₂(— 5; 10; — 1), М ₃(4; 1;11) и М ₄(— 8; — 2; 2).

10. Составить уравнение поверхности, образованной враще­нием эллипса

вокруг оси Ох.

Вариант 10

1. Вектор т, перпендикулярный к оси Oz и к вектору a = {8; —15; 3}, образует острый угол с осью Ох. Зная, что | m | = 51, найти его координаты.

2. Векторы a, b, с, образующие правую тройку, взаимно пер­пендикулярны. Зная, что | а | = 4, | а | = 2, | а | = 3, вычислить abc.

3. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) ху — у² = 0; 2) уz + z ² = 0.

4. На линии найти точку:

1) абсцисса которой равна 3; 2) ордината которой равна 2; 3) аппликата которой равна 8.

5. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 5 х — 3 у + 2 z — 3 = 0.

6. Привести уравнение плоскости к нор­мальному виду:

2 z — 1= 0.

7. Для плоскости вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:

2 х +3 у — 6 z + 4 = 0.

8. Составить каноническое уравнение прямой, проходящей через две данные точки:

(0; 2; —4), (—1; 0; —4).

9. Составить уравнение сферы радиуса r = 3, касающейся плоскости х + 2 у + 2 z +3 = 0 в точке M ₁ (l; 1; — 3).

10. Составить уравнение поверхности, образованной враще­нием гиперболы

вокруг оси Oz.

Дата добавления: 2017-01-14