Система с несколькими серверами

В табл. П4.5 приведены формулы для определения основных параметров в слу­чае работы с системой со множеством серверов. Эти формулы применимы только для случая использования модели M/M/N. То есть предполагается пуассоновский характер распределения времен поступления элементов данных и экспонен­циальный характер времени обслуживания этих элементов. При этом формула Пуассона для распределения времени обслуживания применима для всех N сер­веров. Во всех выражениях используется функция Эрланга С, которая, в одних случаях, определяет вероятность того, что все сервера заняты в определенный момент времени, а в других случаях — вероятность того, что количество элемен­тов данных, находящихся в данный момент времени в системе (ожидающих в очереди или обслуживающихся), будет больше или равно количеству серверов. Для вычисления функции С применима следующая формула:

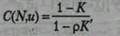
где К — коэффициент пуассоновского распределения.

Значение этой функции зависит от количества серверов (N) и их утилизации (р). Функцию Эрланга приходится часто применять при расчете очередей, что значительно усложняет вычисления. Следует отметить, что для системы с одним сервером эта функция значительно упрощается. А именно: С = (1, и) = р. Такое упрощение как раз и позволяет для системы с одним сервером получить краси­вые законченные формулы (табл. П4.5).

Таблица П4.5. Формулы для определения параметров системы со множеством серверов

Рассмотренная теория очередей достаточно эффективно может быть исполь­зована на практике в различных ситуациях. Приведем пример практического применения теории очередей. Рассмотрим локальную сеть, имеющую в своем составе 100 рабочих станций и один сервер (N = 1), который обслуживает общую базу данных. Среднее время ответа сервера на запрос — 0.6 с. Стандарт­ное отклонение этого времени также равно 0.6 с. В пиковые периоды работы локальной сети скорость поступления запросов к серверу достигает значения 20 запросов в минуту.

Ответим на следующие вопросы:

q Чему равно среднее время ответа сервера?

q Если время ответа, равное 1.5 с, рассматривается как максимально прием­лемое, то насколько может вырасти процент загрузки до достижения на­сыщения сервера?

q Если ожидается, скажем, 20-процентное увеличение утилизации сервера, то насколько увеличится время ответа (на 20 %, больше чем 20 %, меньше чем 20 %)?

Предположим, что в рассматриваемой ситуации применима модель М/М/1. Будем игнорировать задержки, вносимые сетью, полагая, что распределение за­держки в ней можно не принимать в расчет.

Вычислим некоторые параметры сети. Сначала найдем скорость поступления λ:

λ = 20 поступлений в минуту = 20/60 поступлений в секунду = 1/3 поступлений в секунду.

Утилизация сервера вычисляется по формуле:

р = λ Ts = (1/3 поступлений в секунду) (0.6 секунд на передачу) = 0.2. Вычислим среднее время ответа:

Tq ⁼ Ts/(1 -р)= 0.6/(1 - 0.2) = 0.75 с.

На второй вопрос однозначно ответить сложно, так как существует ненулевая вероятность того, что в некоторых случаях время ответа сервера будет превы­шать 1.5 с. Поэтому можно предположить, что в 90 % ответы сервера будут даны менее чем за 1.5 с. Если сделать такое допущение, то мы сможем воспользовать­ся формулой из второго столбца в табл. П4.4:

mTq (r) ⁼ Tq ln(100/(100 - r)).

Получаем:

m-Tq(90) = Tq ln(10) = Ts/(1 - р) 2.3 = 1.5 с.

Учитывая, что Ts = 0.6 с, получаем утилизацию сервера р = 0.008, то есть 8 %. Итак, можно сказать, что при изменении загруженности сервера в диапазоне от 8 % до 20 % (см. выше) время ответа сервера будет менее 1.5 с в 90 % случаев.

В заключение определим зависимость между возрастанием нагрузки и увели­чением времени ответа. Время ответа будет увеличиваться несколько медленнее, чем утилизация. Действительно, в нашем случае, если утилизация сервера воз­росла с 20 % до 40 %, то значение Tq изменится от 0.75 с до 1.0 с (как нетрудно подсчитать), что означает увеличение на 33.3 %.

Дата добавления: 2015-07-13