Питання 2. Основні термінологічні поняття що використовуються при застосуванні методів математичної статистики у психології

Запитання. Завдання.

1. Охарактеризуйте основні розділи математичної статистики.

2. В чому полягає основна ідея математичної статистики?

3. Охарактеризуйте співвідношення генеральної і вибіркової сукупностей.

4. Поясніть схему застосування методів математичної статистики.

5. Укажіть перелік основних завдань математичної статистики.

6. З яких основних блоків складається застосування статистичних методів? Охарактеризуйте їх.

7. Розкрийте зв'язок математичної статистики з теорією ймовірностей.

Статистичні показники, що розкривають властивості вибірки, можна представити такими основними групами:

- емпіричними розподілами (варіаційними, атрибутивними, ранжирова-ними), що характеризують структуру досліджуваної властивості;

- вибірковими показниками (мірами центральної тенденції і мінливості), які представляють чисельні значення типових властивостей вибірки;

- кореляційно-регресійними показниками (коефіцієнтами кореляції, регресії), які дають можливість встановити приховані взаємозв'язки та закономірності явищ, спрогнозувати розвиток досліджуваних процесів.

Емпіричні дані, які отримані шляхом вимірювань властивостей вибіркових об'єктів, повинні пройти первинну обробку і систематизацію: внесення у табличні форми (етап табуляціі), упорядкування у варіаційні послідовності (ряди), представлення у вигляді емпіричних розподілів⁴

Як бачимо, варіаційний ряд - це упорядкована за збільшенням (або за зменшенням) послідовність значень досліджуваної змінної X (у табл. 2.1 значення х/). Варіаційний ряд дає можливість наочно і швидко сприйняти структуру даних: варіанти значень (х), які може приймати і приймає змінна X, а також кількість відповідних варіант (т), їхні мінімальне і максимальне значення. Варіаційний ряд дозволяє безпосередньо оцінити деякі важливі показники вибірки, наприклад, моду і медіану. Систематизація даних у варіаційний ряд є підготовчим етапом до розрахунків і побудови статистичних розподілів досліджуваної змінної.

Статистичний розподіл - це математична модель об'єктів реальності у вигляді співвідношення значень змінної X, що характеризує властивості вибірки, до частот їх появи. Наприклад, стовпчики значень х_і (варіанти X) і значень ті (кількість варіант) у табл. 2.1 по суті утворюють статистичний розподіл, який розкриває залежність частоти появи (/і) від значень (х_і) змінної, тобто / ~ х_і. Отже, під поняттям "статистичний розподіл" /(х) слід розуміти емпіричний розподіли частот появи певних значень досліджуваної змінної (слово "частота" нерідко опускають, маючи на увазі його присутність). Частота / - це функція, де аргументом виступає варіанта х_;.

Статистичні розподіли можна класифікувати за ознакою типів вимірювань⁶ змінної на: варіаційні, ранжировані та атрибутивні (рис. 2.1).

Рис. 2.1. Класифікація статистичних розподілів за типами вимірювань

Варіаційні розподіли базуються на даних, які виміряні за шкалою відношень або інтервалів. Ранжировані розподіли застосовуються у разі порядкових (рангових) типів вимірювання. Атрибутивні розподіли характеризують дані, які виміряні за номінальними шкалами або шкалами "найменувань".

Основні види статистичних розподілів такі: диференціальні та інтегральні, які можуть складатися з абсолютних і відносних частот (рис. 2.2).

Диференціальні розподіли представляють значення частот окремо (тобто диференційовано) для кожної варіанти х,- змінної X.

Диференціальні абсолютні частоти - це кількості об'єктів м_і з однаковими значенням х_і змінної X (або кількість однакових значень).

Диференціальні відносні частоти - це відношення диференціальних абсо-

⁶ Найчастіше використовується класифікація Стівенса 4-х типів вимірювань: за шкалами відношень, інтервалів, порядковими та номінальними [59].

лютних частот ті до загальної кількості п об'єктів, тобто /_і = т_і/п.

Інтегральні розподіли ("накопичені" або "кумулятивні") формуються як доданки попередніх диференціальних частот. Вони визначають сумарні частоти для варіанти, що не перевищує значення х,-змінної X. і

Варіаційні розподіли у разі інтервальних або відносних типів вимірювань залежать від:

o характеру досліджуваної змінної - дискретна змінна, чи неперервна;

o діапазону значень змінної - вузький і невеликий, чи широкий і різноманітний.

Тому за технологією побудови варіаційні розподіли поділяють на розподіли незгрупованих і згрупованих варіант⁷. З метою лаконічності домовимося їх називати незгрупованими і згрупованими розподілами. Для незгрупованих розподілів частоти мають відношення до безпосередніх значень варіант з варіативного ряду; для згрупованих розподілів - до груп (або інтервалів) значень варіант.

Незгруповані розподіли застосовують до емпіричних даних, властивості яких виміряні за інтервальними або відносними шкалами і приймають тільки певні, як правило, дискретні у вузькому діапазоні значення. Процедури розрахунку незгрупованих розподілів простіші за розрахунки розподілів згрупованих.

ля візуалізації результатів використовують графіки, наприклад, відносних диференціальних та інтегральних розподілів рис. 2.3.

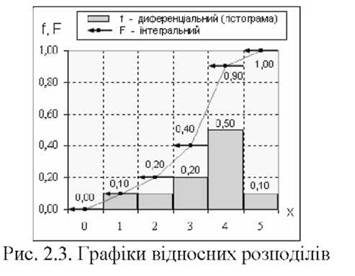
Розподіли відносних частот (диференціальні та інтегральні) мають перевага перед розподілам абсолютних частот, оскільки їхні відносні значення приведені до 100 % і не залежать від обсягу конкретної вибірки.

Отже у результаті систематизації і обробки первинних вибіркових даних формується важливий показник вибірки - емпіричні розподіли частот: диференціальні та інтегральні, кожний з яких може бути або абсолютним, або відносним. Сума всіх абсолютних частот дорівнює обсягу вибірки, сума всіх відносних частот дорівнює 1 або 100%. Інтегральні (накопичені) розподіли формуються як доданки усіх попередніх диференціальних частот або абсолютних, або відносних. Вони дають значення сумарної частоти для варіанти, яка не перевищує значення х,-.

У психолого-педагогічних дослідженнях переважно розраховуються розподіли відносних частот, оскільки саме відносні частоти представляють собою (це буде доведено нижче) і визначаються як статистичні ймовірності.

Крім варіаційних (незгрупованих і згрупованих) розподілів у практиці досліджень розраховують атрибутивні і ранжирувані розподіли, яки використовують для описової характеристики значення так званих "якісних" емпіричних даних, що виміряні за порядковими та номінальними шкалами.

Атрибутивні розподіли використовуються у разі номінальних (категоріальних) типів вимірювань властивостей досліджуваних об'єктів.

Дата добавления: 2015-07-13