
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ТИ – это табличное отражение работы логической схемы, в которой представлены все возможные комбинации значений входных сигналов и соответствующие им значеия выходных сигналов
|
|
|
|
Основные понятия
Алгебра логики – это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.
Логическое высказывание - это любое утверждение, в отношении которого можно однозначно сказать истинно оно или ложно.
Создателем алгебры логики является английский математик Джордж Буль.
Алгебра логики оперирует с логическими переменными, которые могут принимать только два значения – «истина», «ложь», которые обозначаются 1 и 0.
В алгебре логики используются три основные операции – И, ИЛИ, НЕ.
Для реализации этих операций на аппаратном уровне разработаны три логические схемы, которые также называются – И, ИЛИ, НЕ.
С помощью этих элементов можно реализовать любую логическую функцию.
Работу логических элементов описывают с помощью таблиц истинности (ТИ).
| Логический элемент ИЛИ предназначен для реализации функции: выходной сигнал равен 1, если хотя бы один из входных сигналов равен единицы. Входных сигналов может быть два и более, выход только один. | |||||||||||||||||
Условное обозначение на схеме 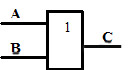
| Для обозначения логической операции ИЛИ используется знак V, операция называется логическое сложение, или дизъюнкция. Примеры записи: С = А V В C = А или В | ТИ
| |||||||||||||||
| Логический элемент И предназначен для реализации функции: выходной сигнал равен 0, если хотя бы один из входных сигналов равен нулю. Входных сигналов может быть два и более, выход только один. | |||||||||||||||||
Условное обозначение на схеме 
| Для обозначения логической операции И используется знак & (/\), операция называется логическое умножение, или конъюнкция. Примеры записи: С = А & В С = А /\ В C = А и В | ТИ
| |||||||||||||||
| Логический элемент НЕ предназначен для получения входного сигнала противоположного входному. Элемент имеет один вход и один выход. | |||||||||||||||||
Условное обозначение на схеме 
| Для обозначения логической операции НЕ используется знак  , операция называется отрицание или инверсия Примеры записи: , операция называется отрицание или инверсия Примеры записи: 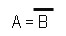 A= не В
Элемент НЕ имеет название инвертор. A= не В
Элемент НЕ имеет название инвертор.
| ТИ
|
| Законы логики | ||||||||||||||||||||||||||||||||||
Для преобразования логических выражений с целью приведения их к нормальной форме используют законы логики.
Некоторые из них имеют аналоги в обычной алгебре.
Правила выполнения операций в сложных логических выражениях: 1. выполняются действия в скобках 2. затем выполняются операции в порядке приоритетности: 1) инверсия 2) конъюнкция 3) дизъюнкция | ||||||||||||||||||||||||||||||||||
| Упрощение логических выражений | ||||||||||||||||||||||
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1)
| ||||||||||||||||||||||
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 513; Нарушение авторских прав?; Мы поможем в написании вашей работы!
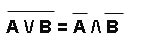

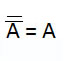




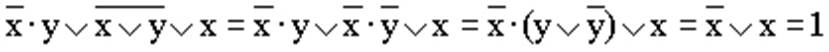


 ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
 5)
5)
 6)
6)
 7)
7)
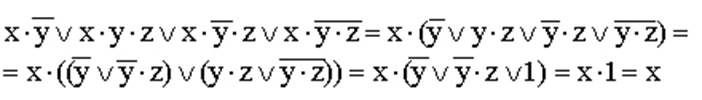 8)
8)
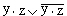 применяется правило операции переменной с её инверсией);
применяется правило операции переменной с её инверсией);
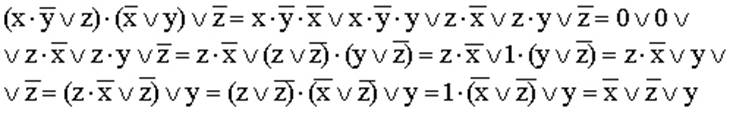 9)
9)
