I. Линейная зависимость

Тем, кто любит смотреть книгу с конца.

Только презентация!

Это то, что сразу дает эффект! Сразу проверьте хотя бы один прием Ключа, что бы убедиться, как действуют эти приемы биокибернетики, и для вас откроется эта книга и перспективы новых возможностей.

Опыт показал — только презентация! Потому что это новое! Это — работает!

Все слова о здоровье, о счастье, о пути к успеху «затасканы», рекламный век наложил свой отпечаток. Поэтому когда нам предлагается что-то новое, то нам кажется, что мы и так все понимаем, и проходим мимо.

Это нас подводят старые ассоциации, старый опыт.

Чтобы открыть для себя новое, нужно обязательно попробовать! Обязательно попробуйте хотя бы один прием Ключа!

И новое откроется...

КЛЮЧ — ЭТО МАЛЕНЬКОЕ НАУЧНОЕ ЧУДО!

Вы уже прочитали эту книгу? Мне кажется, вы к ней еще вернетесь... Буду искренне рад.

Пусть 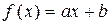, тогда необходимо найти min функции двух переменных: .

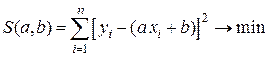По необходимому условию экстремума обе частные производные этой функции двух переменных должны быть равны нулю:

.

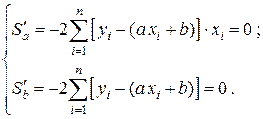Раскрывая скобки, получим систему для определения неизвестных параметров a и b:

.

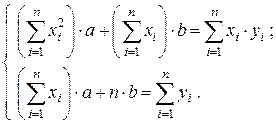Значения коэффициентов при неизвестных a и b определяем из первоначальной таблицы как соответствующие суммы значений переменных х, у.

Решая эту систему относительно коэффициентов a и b:, получим:

,

.

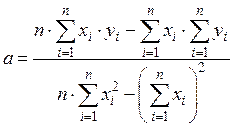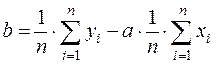Убедимся, что в точке 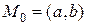функция S(a,b) имеет минимум.

Составим матрицу Гессе и найдем ее главные миноры:

,

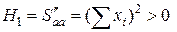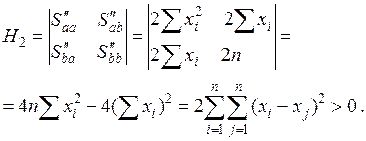
Так как главные миноры матрицы Гессе положительны, то по критерию Сильвестра матрица положительно определена и квадратичная форма второго дифференциала 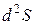, соответствующая этой матрице, принимает только положительные значения.

Из условия 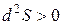следует, что 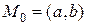- точка минимума.

Если коэффициенты линейной функции найдены, можно вычислить суммарную погрешность: .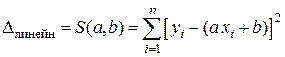

II. Показательная функция .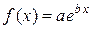

Сведем этот случай к линейной функции.

1. Логарифмируем уравнение: .
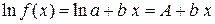2. Логарифмируем таблицу:

			…
			…

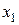
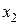
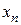
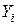
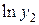
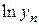
Обозначим 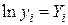, , 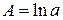тогда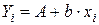

1. Найдем коэффициенты А и b аналогично первому случаю линейной функции:

.

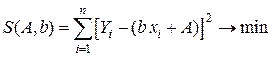Дальнейшие вычисления провести самостоятельно аналогично первому пункту. Окончательное значение коэффициента а определить по формуле .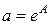

Суммарная погрешность равна .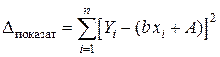

III. Степенная функция .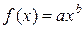

Поступим аналогично показательной функции.

1. Логарифмируем уравнение: 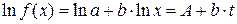, получим - линейную функцию.
2. Логарифмируем таблицу:

			…
			…

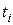
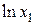
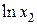
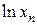
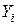
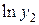
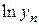
3. Обозначим 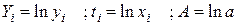. Тогда .

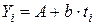Найдем коэффициенты 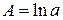и b аналогично первому случаю:

.

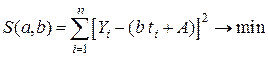Дальнейшие вычисления провести самостоятельно аналогично первому пункту. Окончательное значение коэффициента а определить по формуле .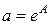

Суммарная погрешность равна .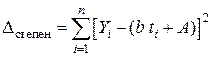

IV. Квадратичная функция .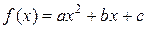

Условие метода наименьших квадратов имеет вид:

.

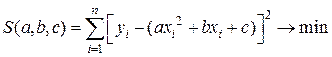Аналогично линейной функции составляется система трех уравнений 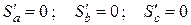, из которой находятся коэффициенты a, b и с:

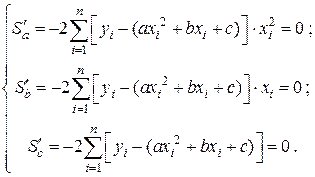
Запишем систему в развернутом виде:

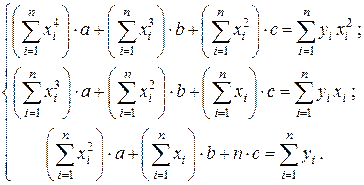
Эта система имеет единственное решение. Кроме того, можно доказать, что коэффициенты, получаемые методом наименьших квадратов, всегда определяют именно минимум функции .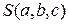

Суммарная погрешность .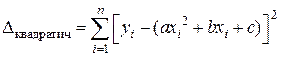

Дата добавления: 2015-07-13