Дизъюнктивные и конъюнктивные нормальные формы

Замечание.

Формулы насыщены скобками и трудночитаемы, поэтому мы примем соглашение об упрощении записи формул:

А) Наружные скобки в записи формул можно опускать;

Б) Условимся, что конъюнкция "сильнее" дизъюнкции, а обе они "сильнее" 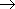и ↔, поэтому часть скобок, определяющих порядок действий, можно опускать.

Конъюнктивным одночленом от переменных х₁, х₂, …,х_n называется конъюнкция этих переменных или их отрицаний.

Дизъюнктивным одночленом от переменных х₁, х₂,..., х_n называется дизъюнкция этих переменных или их отрицаний.

Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных одночленов, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.

Например: ДНФ

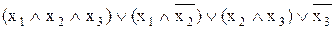
Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных одночленов, называется конъюнктивной нормальной формой (КНФ) данной формулы.

Например: КНФ

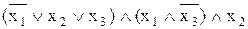
Для каждой формулы алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм.

Дата добавления: 2015-07-13